题目内容
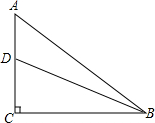 如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=
如图,在Rt△ABC中,∠ACB=90°,D为AC上一点,己知AD=4,AB=15,sinA=| 4 |
| 5 |
考点:解直角三角形,勾股定理
专题:计算题
分析:在直角三角形ABC中,利用锐角三角函数定义及sinA的值求出BC的长,利用勾股定理求出AC的长,由AC-AD求出DC的长,在直角三角形BDC中,利用锐角三角函数定义求出tan∠BDC的值即可.
解答:解:在Rt△ABC中,∠ACB=90°,AD=4,AB=15,sinA=
,
∴sinA=
,即
=
,
可得BC=12,
根据勾股定理得:AC=
=9,
∴DC=AC-AD=9-4=5,
在Rt△BCD中,tan∠BDC=
=
.
| 4 |
| 5 |
∴sinA=
| BC |
| AB |
| BC |
| 15 |
| 4 |
| 5 |
可得BC=12,
根据勾股定理得:AC=
| AB2-BC2 |
∴DC=AC-AD=9-4=5,
在Rt△BCD中,tan∠BDC=
| BC |
| DC |
| 12 |
| 5 |
点评:此题属于解直角三角形题型,涉及的知识有:锐角三角函数定义,勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
下列等式变形正确的是( )
A、如果s=vt,那么v=
| ||
B、如果
| ||
| C、如果x-3=y-3,那么x=y | ||
| D、如果a=b,那么a+b=b-a |
已知△ABC∽△DEF,且AB=2DE,h1,h2分别为AB、DE边上的高线,则
=( )
| h1 |
| h2 |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
 如图,直线y=-x+2
如图,直线y=-x+2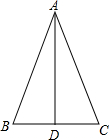 如图,已知△ABC中,点D为BC边上的中点,AB=13,AD=12,BD=5.
如图,已知△ABC中,点D为BC边上的中点,AB=13,AD=12,BD=5.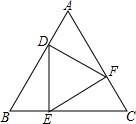 如图所示,在等边△ABC中,D、E、F分别是AB、BC、AC、上的点,DE⊥BC,EF⊥AC,FD⊥AB,BE=3,则△ABC的周长为
如图所示,在等边△ABC中,D、E、F分别是AB、BC、AC、上的点,DE⊥BC,EF⊥AC,FD⊥AB,BE=3,则△ABC的周长为 如图,OC平分∠AOB,∠AOC=20°,P为OC上一点,PD=PE,OD≠OE,∠OPE=110°,则∠ODP=
如图,OC平分∠AOB,∠AOC=20°,P为OC上一点,PD=PE,OD≠OE,∠OPE=110°,则∠ODP=