题目内容
9. 如图,直线CD与直线AB相交于C,根据下列语句画图,并填空:
如图,直线CD与直线AB相交于C,根据下列语句画图,并填空:(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R.
(3)在图中,若∠ACD=65°,则∠PQB=115度,∠RPQ=90度.
分析 (1)平移CD使它经过点P即可得到PQ;
(2)过点P作PR⊥DC于R;
(3)先根据平行线的性质得∠PQA=∠ACD=65°,则利用邻补角计算∠PQB,根据垂直定义得∠PRC=90°,然后利用平行线的性质求∠RPQ=90°.
解答 解:(1)如图,PQ为所作;
(2)如图,PR为所作;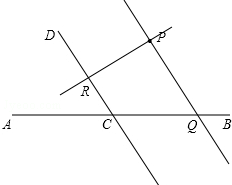
(3)在图中,∵PQ∥CD,
∴∠PQA=∠ACD=65°,
∴∠PQB=180°-65°=115°,
∵PR⊥CD,
∴∠PRC=90°,
∵PQ∥CD,
∴∠RPQ+∠PRC=180°,
∴∠RPQ=90°.
故答案为115,90.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
20.(-0.7)2的平方根是( )
| A. | -0.7 | B. | 0.7 | C. | ±0.7 | D. | 0.49 |
17. 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )
在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )
 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )
在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是$\sqrt{2}$和-1,则点C所对应的实数是( )| A. | 1+$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | 2$\sqrt{2}$+1 |
1.下列各式不能用平方差公式法分解因式的是( )
| A. | x2-4 | B. | -x2-y2+2xy | C. | m2n2-1 | D. | a2-4b2 |
18.圆锥的侧面展开图为半径为16,且圆心角为90°的扇形,则这个圆锥的底面半径为( )
| A. | 16 | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8 |
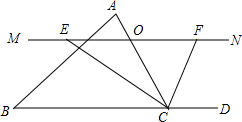 已知△ABC中,点O是边AC上的一个动点,过O做直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
已知△ABC中,点O是边AC上的一个动点,过O做直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F. 如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.
如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.