题目内容
18. 如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.
如图,将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,BC的延长线交DE于F,连接BD,若BC=2EF,试证明△BED是等腰三角形.
分析 根据直角三角形的两锐角互余,以及对顶角相等,旋转的性质,即可证得BF是DE的垂直平分线,据此即可证得.
解答 证明:∵将Rt△ABC绕直角顶点A逆时针旋转90°得到△ADE,
∴DE=BC,∠ADF=∠ABC,
∵BC=2EF,
∴DF=EF,
∴DE=2EF,
∵在直角△ABC中,∠ABC+∠ACB=90°,
又∵∠ABC=∠ADE,
∴∠ACB+∠ADE=90°.
∵∠FCD=∠ACB,
∴∠FCD+∠ADE=90°,
∴∠CFD=90°,
∴BF⊥DE,
∵EF=FD,
∴BF垂直平分DE,
∴BD=BE,
∴△BDE是等腰三角形.
点评 本题考查了旋转的性质,等腰三角形的判定,线段垂直平分线的判定和性质,熟练掌握各定理是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
6. 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )
 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.在-2,0,3,$\sqrt{6}$这四个数中,最大的数是( )
| A. | -2 | B. | 3 | C. | 0 | D. | $\sqrt{6}$ |
7.实数π,0,$\sqrt{5}$,-6其中最大的数是( )
| A. | $\sqrt{5}$ | B. | π | C. | 0 | D. | -6 |

 如图,直线CD与直线AB相交于C,根据下列语句画图,并填空:
如图,直线CD与直线AB相交于C,根据下列语句画图,并填空: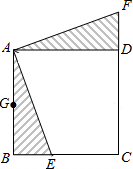 如图,在正方形ABCD中,E是BC上一点,△ABE经过旋转后得到△ADF.
如图,在正方形ABCD中,E是BC上一点,△ABE经过旋转后得到△ADF.