题目内容
19.某体育商店购进一批甲、乙两种足球,已知3个甲种足球的进价与2个乙种足球的进价的和为142元,2个甲种足球的进价与4个乙种足球的进价的和为164元.(1)求每个甲、乙两种足球的进价分别是多少?
(2)如果购进甲种足球超过10个,超出部分可以享受7折优惠.商场决定在甲、乙两种足球选购其中一种,且数量超过10个,试帮助体育商场判断购进哪种足球省钱.
分析 (1)设每件甲种足球的进价是x元,每件乙种足球的进价是y元,根据“3个甲种足球的进价与2个乙种足球的进价的和为142元,2个甲种足球的进价与4个乙种足球的进价的和为164元”列出方程组解决问题;
(2)设购进足球z件(z>10),分别表示出甲种和乙种足球消费,建立不等式解决问题.
解答 解:(1)设甲种足球的进价是x元,乙种足球的进价是y元,由题意得:
$\left\{\begin{array}{l}{3x+2y=142\\;}\\{2x+4y=164}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=30}\\{y=26}\end{array}\right.$.
答:甲种足球的进价是30元,乙种足球的进价是26元;
(2)设购进足球z个(z>10),则乙种足球消费26z元,甲种足球消费10×30+(z-10)×30×0.7元,
①当26z=10×30+(z-10)×30×0.7,
解得z=18.
所以当购进足球正好18个,选择购其中一种即可;
②当26z>10×30+(z-10)×30×0.7,
解得z>18.
所以当购进足球超过18个,选择购甲种足球省钱;
③当26z<10×30+(z-10)×30×0.7,
解得z<18.
所以当购进足球少于18个,多于10个,选择购乙种足球省钱.
点评 此题主要考查二元一次方程组,一元一次不等式的运用,关键是理解题意,找出题目中的等量关系和不等关系,列出方程和不等式.

练习册系列答案
相关题目
8.一个扇形的圆心角是120°,面积为3πcm2,那么这个扇形的半径是( )
| A. | 1cm | B. | 3cm | C. | 6cm | D. | 9cm |
11.Rt△ABC中,两直角边的长分别为6和8,则其斜边上的中线长为( )
| A. | 10 | B. | 3 | C. | 4 | D. | 5 |
9. 如图所示是一个几何体的三视图,则这个几何体的名称是( )
如图所示是一个几何体的三视图,则这个几何体的名称是( )
 如图所示是一个几何体的三视图,则这个几何体的名称是( )
如图所示是一个几何体的三视图,则这个几何体的名称是( )| A. | 圆柱 | B. | 圆锥 | C. | 长方体 | D. | 棱锥 |
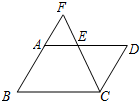 如图,E是?ABCD的AD边上一点,CE与BA的延长线交于点F,则下列比例式:①$\frac{FB}{CD}$=$\frac{FC}{CE}$;②$\frac{AE}{ED}$=$\frac{AF}{AB}$;③$\frac{FA}{FB}$=$\frac{AE}{AD}$;④$\frac{AE}{EC}$=$\frac{FE}{ED}$,其中一定成立的是( )
如图,E是?ABCD的AD边上一点,CE与BA的延长线交于点F,则下列比例式:①$\frac{FB}{CD}$=$\frac{FC}{CE}$;②$\frac{AE}{ED}$=$\frac{AF}{AB}$;③$\frac{FA}{FB}$=$\frac{AE}{AD}$;④$\frac{AE}{EC}$=$\frac{FE}{ED}$,其中一定成立的是( ) 如图,P为正方形ABCD内一点,且BP=2,PC=3,∠APB=135°,将△APB绕点B顺时针旋转90°得到△CP′B,连接PP′,则AP=1.
如图,P为正方形ABCD内一点,且BP=2,PC=3,∠APB=135°,将△APB绕点B顺时针旋转90°得到△CP′B,连接PP′,则AP=1.