题目内容
7.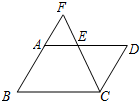 如图,E是?ABCD的AD边上一点,CE与BA的延长线交于点F,则下列比例式:①$\frac{FB}{CD}$=$\frac{FC}{CE}$;②$\frac{AE}{ED}$=$\frac{AF}{AB}$;③$\frac{FA}{FB}$=$\frac{AE}{AD}$;④$\frac{AE}{EC}$=$\frac{FE}{ED}$,其中一定成立的是( )
如图,E是?ABCD的AD边上一点,CE与BA的延长线交于点F,则下列比例式:①$\frac{FB}{CD}$=$\frac{FC}{CE}$;②$\frac{AE}{ED}$=$\frac{AF}{AB}$;③$\frac{FA}{FB}$=$\frac{AE}{AD}$;④$\frac{AE}{EC}$=$\frac{FE}{ED}$,其中一定成立的是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ①② |
分析 根据平行四边形的性质得到AB=CD,AD=BC,AB∥CD,AD∥BC,根据平行线分线段成比例定理得到$\frac{BF}{AB}=\frac{CF}{CE}$,即$\frac{FB}{CD}$=$\frac{FC}{CE}$;根据相似三角形的性质得到$\frac{AE}{ED}=\frac{AF}{CD}$,即$\frac{AE}{ED}$=$\frac{AF}{AB}$,根据相似三角形的性质得到$\frac{FA}{FB}=\frac{AE}{BC}$,即$\frac{FA}{FB}$=$\frac{AE}{AD}$.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AB∥CD,AD∥BC,
∴$\frac{BF}{AB}=\frac{CF}{CE}$,即$\frac{FB}{CD}$=$\frac{FC}{CE}$;故①正确;
∵AB∥CD,
∴△AEF∽△CDE,
∴$\frac{AE}{ED}=\frac{AF}{CD}$,即$\frac{AE}{ED}$=$\frac{AF}{AB}$,故②正确;
∵AE∥BC,
∴△AEF∽△FBC,
∴$\frac{FA}{FB}=\frac{AE}{BC}$,即$\frac{FA}{FB}$=$\frac{AE}{AD}$,故③正确;
∵AF∥CD,
∴$\frac{AE}{DE}=\frac{EF}{CE}$,故④错误,
故选B.
点评 此题主要考查了平行四边形的性质和相似三角形的判定与性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
2.某校有200名学生,要想了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从这2000名学生中抽取了100名学生进行调查,在这次调查中,数据100是( )
| A. | 总体 | B. | 总体的一个样本 | C. | 样本容量 | D. | 全面调查 |
17. 如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
 如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )| A. | 70° | B. | 100° | C. | 140° | D. | 170° |
 如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
如图,已知⊙O,用尺规作⊙O的内接正四边形ABCD.(写出结论,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑) 如图,AB是⊙O的直径,C、D是圆上的两点,若BC=8,cos∠D=$\frac{2}{3}$,则AB的长为12.
如图,AB是⊙O的直径,C、D是圆上的两点,若BC=8,cos∠D=$\frac{2}{3}$,则AB的长为12.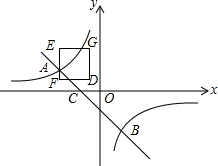 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(-2,1),点B(1,n).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(-2,1),点B(1,n). 如图,直线y=kx与双曲线y=-$\frac{2}{x}$交于A(x1,y1),B(x2,y2)两点,则2x1y2-8x2y1的值为( )
如图,直线y=kx与双曲线y=-$\frac{2}{x}$交于A(x1,y1),B(x2,y2)两点,则2x1y2-8x2y1的值为( )