题目内容
4．若$\frac{x}{y}$=3，求（1+$\frac{{y}^{2}}{{x}^{2}-{y}^{2}}$）÷$\frac{x}{x-y}$的值．分析 原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，把已知等式变形后代入计算即可求出值．
解答 解：原式=$\frac{{x}^{2}-{y}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$•$\frac{x-y}{x}$=$\frac{{x}^{2}}{（x+y）（x-y）}$•$\frac{x-y}{x}$=$\frac{x}{x+y}$，
由$\frac{x}{y}$=3，得到x=3y，
则原式=$\frac{3y}{4y}$=$\frac{3}{4}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
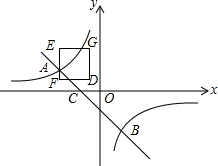如图，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A（-2，1），点B（1，n）．
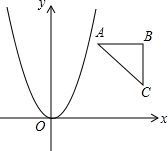已知Rt△ABC的顶点坐标为A（1，2），B（2，2），C（2，1），若抛物线y=ax2与该直角三角形无公共点，则a的取值范围是a＜0或a＞2或0＜a＜$\frac{1}{4}$．
如图，直线y=kx与双曲线y=-$\frac{2}{x}$交于A（x1，y1），B（x2，y2）两点，则2x1y2-8x2y1的值为（ ）
13．下列运算正确的是（ ）
| A． | x4+x4=x8 | B． | （x-y）2=x2-y2 | C． | x3•x4=x7 | D． | （2x2）3=2x6 |
如图，如果圆内接四边形ABCD两组对边的延长线分别相交于点E，F，且∠E=40°，∠F=60°，那么∠A=40°．