题目内容
15.(1)若10x=3,10y=2,求代数式103x+4y的值.(2)已知:3m+2n-6=0,求8m•4n的值.
分析 (1)直接利用同底数幂的乘法运算法则将原式变形求出答案;
(2)直接利用同底数幂的乘法运算法则将原式变形求出答案.
解答 解:(1)∵10x=3,10y=2,
∴代数式103x+4y=(10x)3×(10y)4
=33×24
=432;
(2)∵3m+2n-6=0,
∴3m+2n=6,
∴8m•4n=23m•22n=23m+2n=26=64.
点评 此题主要考查了同底数幂的乘法运算以及幂的乘方运算,正确掌握运算法则是解题关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
6.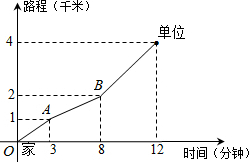 王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )
王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )
 王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )
王老师从家门口骑车去单位上班,先走平路到达A地,再上坡到达B地,最后下坡到达工作单位,所用的时间与路程的关系如图所示.若王老师下班时,还沿着这条路返回家中,回家途中经过平路、上坡、下坡的速度不变,那么王老师回家需要的时间是( )| A. | 15分钟 | B. | 14分钟 | C. | 13分钟 | D. | 12分钟 |
4.为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13-10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
(1)该市规定用水量为8吨,规定用量内的收费标准是2元/吨,超过部分的收费标准是3元/吨.
(2)若小明家五月份用水20吨,则应缴水费52元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
| 月份 | 一 | 二 | 三 | 四 |
| 用水量(吨) | 6 | 7 | 12 | 15 |
| 水费(元) | 12 | 14 | 28 | 37 |
(2)若小明家五月份用水20吨,则应缴水费52元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
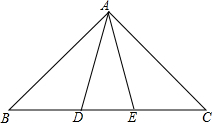 如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.
如图,△ABC中,AB=AC,点D,E在边BC上,且BD=CE.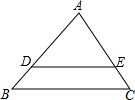 如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC,$\frac{AD}{BD}$=$\frac{3}{2}$,DE=6,则BC的长为( )
如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC,$\frac{AD}{BD}$=$\frac{3}{2}$,DE=6,则BC的长为( ) 如图,在矩形ABCD中,AB=2,∠ADB=30°,沿对角线BD折叠,使△ABD和△EBD落在同一平面内,则A,E之间的距离为2.
如图,在矩形ABCD中,AB=2,∠ADB=30°,沿对角线BD折叠,使△ABD和△EBD落在同一平面内,则A,E之间的距离为2.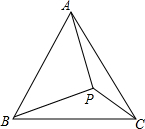 如图,P为等边三角形ABC内一点,PC=3,PA=4,PB=5,求∠APC的度数.
如图,P为等边三角形ABC内一点,PC=3,PA=4,PB=5,求∠APC的度数.