题目内容
10.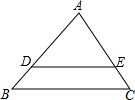 如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC,$\frac{AD}{BD}$=$\frac{3}{2}$,DE=6,则BC的长为( )
如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC,$\frac{AD}{BD}$=$\frac{3}{2}$,DE=6,则BC的长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
分析 根据相似三角形的性质可得$\frac{DE}{BC}$=$\frac{AD}{AB}$,再根据$\frac{AD}{BD}$=$\frac{3}{2}$,DE=6,即可得出$\frac{6}{BC}$=$\frac{3}{5}$,进而得到BC长.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$,
又∵$\frac{AD}{BD}$=$\frac{3}{2}$,DE=6,
∴$\frac{6}{BC}$=$\frac{3}{5}$,
∴BC=10,
故选:C.
点评 本题主要考查了相似三角形的判定与性质的运用,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.

练习册系列答案
相关题目
1.若方程组$\left\{\begin{array}{l}{x+2y=1+m}\\{2x+y=3}\end{array}\right.$中,若未知数x,y满足x+y>0,则m的取值范围是( )
| A. | m≥-4 | B. | m>-4 | C. | m<-4 | D. | m≤-4 |
5.王华五次数学考试成绩分别为:86分,78分,80分,85分,92分,李老师想了解他数学成绩的稳定情况,则应关注王华数学成绩的( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
19.某废品收购站为了鼓励市民回收废品,如果一次回收2千克以上的废旧报纸,那么超过2千克部分的废旧报纸每千克比原价多付20%,根据下表,回答下列问题:
(1)回收1千克废旧报纸的价格是0.5元;
(2)设收购废旧报纸的质量为x千克,付款全额为y元,求y关于x的函数表达式;
(3)若小明在废品收购站卖废旧报纸一次性获得5.8元,那么他回收了多少废旧报纸?
| 回收废旧报纸的质量/千克 | 1.5 | 2 | 3.5 | 4 | … |
| 付款全额/元 | 0.75 | 1.0 | 1.9 | 2.2 | … |
(2)设收购废旧报纸的质量为x千克,付款全额为y元,求y关于x的函数表达式;
(3)若小明在废品收购站卖废旧报纸一次性获得5.8元,那么他回收了多少废旧报纸?
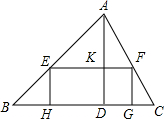 在锐角△ABC中,边BC长为18,高AD长为12
在锐角△ABC中,边BC长为18,高AD长为12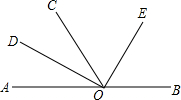 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC.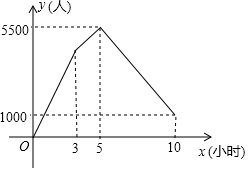 国家“5A”级景区某日迎来客流高峰,从索道开始运行前3小时开始,每小时都有a名游客源源不断地涌入候客大厅排队.索道每小时运送b名游客上山,索道运行2小时后,景区调来若干辆汽车和索道一起送游客上山,其中每小时有$\frac{7}{5}$b名游客乘坐汽车上山.5小时后,在候客大厅排队的游客人数降至1000人,候客大厅排队的游客人数y(人)与游客开始排队后的时间x(小时)之间的关系如图所示.则a=1500.
国家“5A”级景区某日迎来客流高峰,从索道开始运行前3小时开始,每小时都有a名游客源源不断地涌入候客大厅排队.索道每小时运送b名游客上山,索道运行2小时后,景区调来若干辆汽车和索道一起送游客上山,其中每小时有$\frac{7}{5}$b名游客乘坐汽车上山.5小时后,在候客大厅排队的游客人数降至1000人,候客大厅排队的游客人数y(人)与游客开始排队后的时间x(小时)之间的关系如图所示.则a=1500.