题目内容
6．
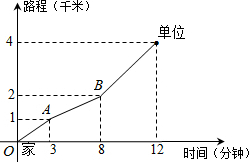王老师从家门口骑车去单位上班，先走平路到达A地，再上坡到达B地，最后下坡到达工作单位，所用的时间与路程的关系如图所示．若王老师下班时，还沿着这条路返回家中，回家途中经过平路、上坡、下坡的速度不变，那么王老师回家需要的时间是（ ）| A． | 15分钟 | B． | 14分钟 | C． | 13分钟 | D． | 12分钟 |
分析 依据图象分别求出平路、上坡路和下坡路的速度，然后根据路程，求出时间即可．
解答 解：先算出平路、上坡路和下坡路的速度分别为$\frac{1}{3}$、$\frac{1}{5}$和$\frac{1}{2}$（千米/分），
所以他从单位到家门口需要的时间是2÷$\frac{1}{5}$+1÷$\frac{1}{2}$+1÷$\frac{1}{3}$=15（分钟）．
故选：A．
点评 本题考查了一次函数的应用，通过考查一次函数的应用来考查从图象上获取信息的能力．
练习册系列答案
新思维寒假作业系列答案
相关题目
1．若方程组$\left\{\begin{array}{l}{x+2y=1+m}\\{2x+y=3}\end{array}\right.$中，若未知数x，y满足x+y＞0，则m的取值范围是（ ）
| A． | m≥-4 | B． | m＞-4 | C． | m＜-4 | D． | m≤-4 |
11．某公司在销售一种产品进价为10元的产品时，每年总支出为10万元（不含进货支出），经过若干年销售得知，年销售量y（万件）是销售单价x（元）的一次函数，并得到如下部分数据；
（1）求出y关于x的函数关系式是y=-$\frac{1}{2}$x+13；
（2）写出该公司销售这种产品的年利润w（万元）关于销售单价x（元）的函数关系式；当销售单价x为何值时，年利润最大？
（3）试通过（2）中的函数关系式及其大致图象，帮助该公司确定产品的销售单价范围，使年利润不低于20万元（请直接写出销售单价x的范围）．
| 销售单价x（元） | 12 | 14 | 16 | 18 |
| 年销售量y（万件） | 7 | 6 | 5 | 4 |
（2）写出该公司销售这种产品的年利润w（万元）关于销售单价x（元）的函数关系式；当销售单价x为何值时，年利润最大？
（3）试通过（2）中的函数关系式及其大致图象，帮助该公司确定产品的销售单价范围，使年利润不低于20万元（请直接写出销售单价x的范围）．
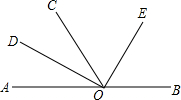如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC．