题目内容
10．已知n为正整数，对于给定的正实数m，是否存在n，使关于x的方程x2-2$\sqrt{m}$x+2n=0有两个相等的实数根？如果存在，用m的代数式表示n；如果没有，说明理由．分析 由方程有两个相等实数根可得△=0，用含m的式子表示n即可．
解答 解：根据题意知，△=（-2$\sqrt{m}$）2-4×2n=4m-8n=0，
即n=$\frac{1}{2}$m，
故对于给定的正实数m，当n=$\frac{1}{2}$m时，方程有两个相等的实数根．
点评 本题主要考查一元二次方程根的判别式，解题关键是了解根的判别式如何决定一元二次方程根的情况．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如图，直线l1∥l2，∠2=40°，则∠1+∠3+∠4=220°．
（1）设二次函数y=ax2+bx+c（a≠0）图象如图所示，经过点（-1，0），试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号
如图是一个物体的三视图，根据图中尺寸（单位：cm），它的体积为32+8πcm3．
19．
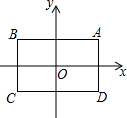如图，坐标原点O为矩形ABCD的对称中心，顶点A的坐标为（1，t），AB∥x轴，矩形A′B′C′D′与矩形ABCD是位似图形，点O为位似中心，点A′，B′分别是点A，B的对应点，且A′B′=2AB．已知mn=3（m，n为正实数），在以m，n为坐标（记为（m，n）的所有的点中，若有且只有一个点落在矩形A′B′C′D′的边上，则t的值等于（ ）
如图，坐标原点O为矩形ABCD的对称中心，顶点A的坐标为（1，t），AB∥x轴，矩形A′B′C′D′与矩形ABCD是位似图形，点O为位似中心，点A′，B′分别是点A，B的对应点，且A′B′=2AB．已知mn=3（m，n为正实数），在以m，n为坐标（记为（m，n）的所有的点中，若有且只有一个点落在矩形A′B′C′D′的边上，则t的值等于（ ）| A． | $\frac{3}{4}$ | B． | 1 | C． | $\frac{4}{3}$ | D． | $\frac{3}{2}$ |
