题目内容
12. 如图,在正方形ABCD中,以CD为边向外作等边三角形CDE,连结AE、BE,则∠AEB=30°.
如图,在正方形ABCD中,以CD为边向外作等边三角形CDE,连结AE、BE,则∠AEB=30°.
分析 欲求∠AEB,只要求出∠BAE,∠ABE的大小即可,只要证明△ADE是顶角为150°的等腰三角形即可解决问题.
解答 解: ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=DC=AD,∠ADC=∠DAB=∠ABC=∠DCB=90°,
∵△CDE是等边三角形,
∴∠CDE=∠DCE=60°,DE=DC=CE,
∴∠ADE=∠ADC+∠CDE=150°,
∵DA=DE,
∴∠DAE=∠DEA=15°,
∴∠BAE=∠BAD-∠DAE=75°,
同理可得∠ABE=75°,
∴∠AEB=180°-∠EAB-∠EBA=30°,
故答案为30.
点评 本题考查正方形的性质.等边三角形的性质、等腰三角形的性质、三角形内角和定理等知识,解题的关键是灵活应用这些知识解决问题,属于基础题.中考常考题型.

练习册系列答案
相关题目
20.下列图案既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列交通标志中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,是二元一次方程2x+ay=3的一个解,则a的值为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 1 | D. | -1 |
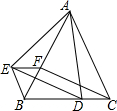 如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF. 如图,在?ABCD中,∠ABC的平分线BM交CD于点M,且MC=2,?ABCD的周长是14,则DM等于3.
如图,在?ABCD中,∠ABC的平分线BM交CD于点M,且MC=2,?ABCD的周长是14,则DM等于3. 如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.
如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.