题目内容
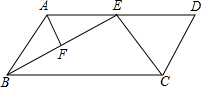 如图,AB∥CD,BC∥AD,BE、CE分别是∠ABC、∠BCD的平分线,F是BE的中点.
如图,AB∥CD,BC∥AD,BE、CE分别是∠ABC、∠BCD的平分线,F是BE的中点.(1)试判断△ABE与△BEC的形状,请说明理由.
(2)试说明AF∥CE的理由.
考点:平行线的判定与性质,等腰三角形的判定
专题:计算题
分析:(1)△ABE为等腰三角形,△BEC为直角三角形,理由为:由BE为角平分线得到一对角相等,由AD与BC平行得到一对内错角相等,等量代换得到∠ABE=∠AEB,利用等角对等边得到AB=AE,即三角形ABE为等腰三角形;由AB与CD平行,得到一对同旁内角互补,由BE与CE都为角平分线,利用等式的性质得到∠EBC+∠ECB=90°,即∠BEC=90°,即三角形BEC为直角三角形;
(2)由直角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
(2)由直角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答:解:(1)△ABE为等腰三角形,△BEC为直角三角形,理由为:
∵BE平分∠ABC,
∴∠ABE=∠CBE=
∠ABC,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∴△ABE为等腰三角形;
∵CE平分∠DCB,BE平分∠ABC,
∴∠ECB=
∠BCD,∠CBE=
∠ABC,
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
∴△BEC为直角三角形;
(2)∵AB=AE,F是中点,
∴AF⊥BE,且CE⊥BE,
∴∠AFE=∠CEF=90°,
∴AF∥CE.
∵BE平分∠ABC,
∴∠ABE=∠CBE=
| 1 |
| 2 |
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∴△ABE为等腰三角形;
∵CE平分∠DCB,BE平分∠ABC,
∴∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
∴△BEC为直角三角形;
(2)∵AB=AE,F是中点,
∴AF⊥BE,且CE⊥BE,
∴∠AFE=∠CEF=90°,
∴AF∥CE.
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
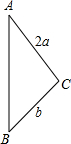 如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )
如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )| A、2πa2 |
| B、πab |
| C、3πa2+πab |
| D、πa(2a+b) |
 如图所示,某地新建一座石拱桥,桥拱是圆弧形,它的跨度(弧所对的弦的长)为40m,拱高(弧的中点到弦的距离)为8m,求桥拱得半径R.
如图所示,某地新建一座石拱桥,桥拱是圆弧形,它的跨度(弧所对的弦的长)为40m,拱高(弧的中点到弦的距离)为8m,求桥拱得半径R.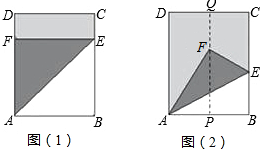 在一张长方形纸片ABCD中,AD=5cm,AB=4cm,现将这张纸片按图示方式折叠,请分别求出折痕的长.
在一张长方形纸片ABCD中,AD=5cm,AB=4cm,现将这张纸片按图示方式折叠,请分别求出折痕的长.