题目内容
 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,点M,P,N,Q分别在AO,BO,CO,DC上,且AM=BP=CN=DQ.求证:四边形MPNQ是矩形.
已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,点M,P,N,Q分别在AO,BO,CO,DC上,且AM=BP=CN=DQ.求证:四边形MPNQ是矩形.考点:矩形的判定与性质
专题:证明题
分析:证明MP∥AB;同理可证QN∥CD;证明MP∥QN,MQ∥PN,得到四边形MPNQ是平行四边形;证明∠MPN=90°即可解决问题.
解答:解:∵四边形ABCD是矩形,
∴∠ABC=90°;AC=BD,AO=
AC,BO=
BD;
∴AO=BO;而AM=BP,
∴AM:AO=BP:BO,
∴MP∥AB;同理可证:QN∥CD;
∵AB∥CD,
∴MP∥QN;同理可证:MQ∥PN,
∴四边形MPNQ是平行四边形;
∵MP∥AB,PN∥BC,∠ABC=90°,
∴∠MPN=90°,
∴四边形MPNQ是矩形.
∴∠ABC=90°;AC=BD,AO=
| 1 |
| 2 |
| 1 |
| 2 |
∴AO=BO;而AM=BP,
∴AM:AO=BP:BO,
∴MP∥AB;同理可证:QN∥CD;
∵AB∥CD,
∴MP∥QN;同理可证:MQ∥PN,
∴四边形MPNQ是平行四边形;
∵MP∥AB,PN∥BC,∠ABC=90°,
∴∠MPN=90°,
∴四边形MPNQ是矩形.
点评:该题主要考查了矩形的判定及其性质的应用问题;灵活运用矩形的判定及其性质是解题的关键关键;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
相关题目
下列长度的三条线段能组成三角形的是( )
| A、1cm,2cm,3cm |
| B、3cm,7cm,3cm |
| C、2cm,4cm,6cm |
| D、4cm,5cm,6cm |
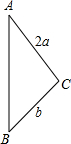 如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )
如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )| A、2πa2 |
| B、πab |
| C、3πa2+πab |
| D、πa(2a+b) |
 如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“魅”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“魅”相对的面上的汉字是( ) 如图,A,B,C在同一直线上,△ABD,△BCE都是等边三角形,AE交BD于点E,DC交BE于点G,求证:BF=BG.
如图,A,B,C在同一直线上,△ABD,△BCE都是等边三角形,AE交BD于点E,DC交BE于点G,求证:BF=BG. 在△ABC中,∠C=90,AD是∠BAC的平分线,BC为切线,DB=5,CD=3,求:AC的长.
在△ABC中,∠C=90,AD是∠BAC的平分线,BC为切线,DB=5,CD=3,求:AC的长.