题目内容
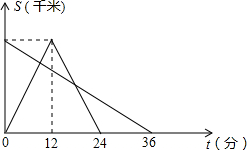 甲、乙两车同时分别从A、B两地出发相向而行,甲车到达B地后立即返回A地,若两车离A地的距离S(千米)与所用时间t(分)的函数关系如图,则甲、乙两车在途中两次相遇的间隔时间为
甲、乙两车同时分别从A、B两地出发相向而行,甲车到达B地后立即返回A地,若两车离A地的距离S(千米)与所用时间t(分)的函数关系如图,则甲、乙两车在途中两次相遇的间隔时间为考点:一次函数的应用
专题:
分析:观察图象得到A与B距离为36千米,确定出P,G,M,N的坐标,利用待定系数法确定出直线OP,直线PN,以及直线GM的解析式,进而确定出Q与R的横坐标,求出两横坐标之差即为所求.
解答: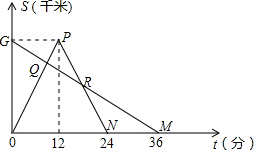 解:设A与B两地的距离为36,可得G(0,d),M(36,0),N(24,0),P(12,36),
解:设A与B两地的距离为36,可得G(0,d),M(36,0),N(24,0),P(12,36),
设直线GM解析式为S=mt+n,
将G与M坐标代入得:
,
解得:
,
∴直线GM解析式为S=-t+36,
设直线OP解析式为S1=kt,
将P坐标代入得:k=3,即直线OP解析式为S1=3t,
联立S与S1消去S得:-t+36=3t,
解得:t=9;
设直线PN解析式为S2=pt+q,
将P与N坐标代入得:
解得:
,
∴直线PN解析式为S2=-3t+72,
联立S与S2消去S得:-t+36=-3t+72,
解得:t=18,
则两车在行驶途中两次相遇的间隔时间为18-9=9(分钟).
故答案为:9.
 解:设A与B两地的距离为36,可得G(0,d),M(36,0),N(24,0),P(12,36),
解:设A与B两地的距离为36,可得G(0,d),M(36,0),N(24,0),P(12,36),设直线GM解析式为S=mt+n,
将G与M坐标代入得:
|
解得:
|
∴直线GM解析式为S=-t+36,
设直线OP解析式为S1=kt,
将P坐标代入得:k=3,即直线OP解析式为S1=3t,
联立S与S1消去S得:-t+36=3t,
解得:t=9;
设直线PN解析式为S2=pt+q,
将P与N坐标代入得:
|
解得:
|
∴直线PN解析式为S2=-3t+72,
联立S与S2消去S得:-t+36=-3t+72,
解得:t=18,
则两车在行驶途中两次相遇的间隔时间为18-9=9(分钟).
故答案为:9.
点评:此题考查了一次函数的应用,利用了待定系数法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
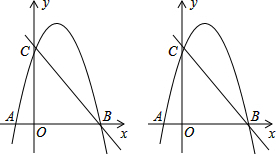
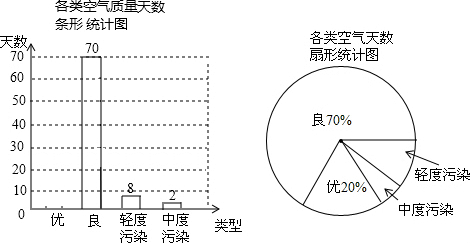

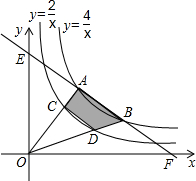 已知,如图,双曲线y=
已知,如图,双曲线y=