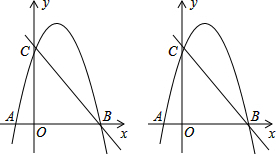题目内容
如图,已知抛物线y=ax2+bx+2(a≠0)与x轴交于A(1,0)、B(4,0)两点,与y轴交于点C,连接AC、BC.
(1)点C的坐标是 ;
(2)求抛物线y=ax2+bx+2(a≠0)的解析式;
(3)若点P在抛物线上,且点P与△ABC的两个顶点所构成的三角形面积S=S△ABC,请求出满足条件的所有点P的坐标.
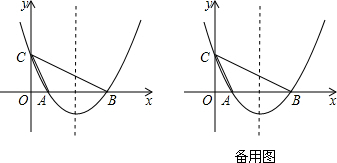
(1)点C的坐标是
(2)求抛物线y=ax2+bx+2(a≠0)的解析式;
(3)若点P在抛物线上,且点P与△ABC的两个顶点所构成的三角形面积S=S△ABC,请求出满足条件的所有点P的坐标.

考点:抛物线与x轴的交点,二次函数图象上点的坐标特征,待定系数法求二次函数解析式
专题:
分析:(1)因为点C的横坐标等于零,且点C位于抛物线上,所以令y=0,则求得点C的纵坐标;
(2)将A(1,0)、B(4,0)点坐标代入抛物线y=ax2+bx+2(a≠0)中,列方程组求a、b的值即可;
(3)所求的P的纵坐标与点C的纵坐标的绝对值相等,所以把相应的y值代入函数解析式来求x的值.
(2)将A(1,0)、B(4,0)点坐标代入抛物线y=ax2+bx+2(a≠0)中,列方程组求a、b的值即可;
(3)所求的P的纵坐标与点C的纵坐标的绝对值相等,所以把相应的y值代入函数解析式来求x的值.
解答: 解:(1)如图,∵点C在抛物线y=ax2+bx+2(a≠0)上,
解:(1)如图,∵点C在抛物线y=ax2+bx+2(a≠0)上,
∴当x=0时,y=2,
∴C(0,2);
故答案是:(0,2);
(2)A(1,0)、B(4,0)两点代入y=ax2+bx+2,得
,
解得
.
则该抛物线的解析式为:y=
x2-
x+2;
(3)情况一:当S△PAB=S△ABC时.点P是平行于x轴且到x轴的距离为2的直线与抛物线的交点.如图1所示.
∵C(0,2),S=S△ABC,
∴设P(x,2)或(x,-2).
①当点P的坐标是(x,2)时,2=
x2-
x+2
解得 x=0或x=5.
则点P的坐标是(0,2)(与点C重合)或(5,2);
②当点P的坐标是(x,-2)时,-2=
x2-
x+2,
∵△<0,
∴该方程无解,即不存在这样的点P.
情况二:当S△PBC=S△ABC时.点P是平行于BC且到BC的距离为点A到BC的距离的直线与抛物线的交点.如图2所示.
易求符合条件的点P的坐标为:(1,0),(3,-1),(2+
,
),(2-
,
);
情况三:当S△PAC=S△ABC时.点P是平行于AC且到AC的距离为点B到AC的距离的直线与抛物线的交点.过点B与AC平行的直线解析式为y=-2x+8,与抛物线联立方程组可求得两根分别为4和-3,此时两点坐标分别为(4,0)(-3,14)
此时当点P与点B重合时,符合题意.
综上所述,符合条件的点P的坐标是:(0,2)或(5,2)或(1,0),((3,-1)或(2+
,
)或
(2-
,
)或(4,0)或(-3,14).
 解:(1)如图,∵点C在抛物线y=ax2+bx+2(a≠0)上,
解:(1)如图,∵点C在抛物线y=ax2+bx+2(a≠0)上,∴当x=0时,y=2,
∴C(0,2);
故答案是:(0,2);
(2)A(1,0)、B(4,0)两点代入y=ax2+bx+2,得
|

解得
|
则该抛物线的解析式为:y=
| 1 |
| 2 |
| 5 |
| 2 |
(3)情况一:当S△PAB=S△ABC时.点P是平行于x轴且到x轴的距离为2的直线与抛物线的交点.如图1所示.
∵C(0,2),S=S△ABC,
∴设P(x,2)或(x,-2).

①当点P的坐标是(x,2)时,2=
| 1 |
| 2 |
| 5 |
| 2 |
解得 x=0或x=5.
则点P的坐标是(0,2)(与点C重合)或(5,2);
②当点P的坐标是(x,-2)时,-2=
| 1 |
| 2 |
| 5 |
| 2 |
∵△<0,
∴该方程无解,即不存在这样的点P.
情况二:当S△PBC=S△ABC时.点P是平行于BC且到BC的距离为点A到BC的距离的直线与抛物线的交点.如图2所示.
易求符合条件的点P的坐标为:(1,0),(3,-1),(2+
| 7 |
5-
| ||
| 2 |
| 7 |
5+
| ||
| 2 |
情况三:当S△PAC=S△ABC时.点P是平行于AC且到AC的距离为点B到AC的距离的直线与抛物线的交点.过点B与AC平行的直线解析式为y=-2x+8,与抛物线联立方程组可求得两根分别为4和-3,此时两点坐标分别为(4,0)(-3,14)
此时当点P与点B重合时,符合题意.
综上所述,符合条件的点P的坐标是:(0,2)或(5,2)或(1,0),((3,-1)或(2+
| 7 |
5-
| ||
| 2 |
(2-
| 7 |
5+
| ||
| 2 |
点评:本题考查了抛物线与x轴的交点,二次函数图象上点的坐标特征以及待定系数法求二次函数解析式.解答(3)题时,要分类讨论.

练习册系列答案
相关题目
 如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则cos∠CGD=( )
如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则cos∠CGD=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|