题目内容
15.⊙O的直径为2,弦AB的长为1,弦BC的长为$\sqrt{2}$,则∠ABC的度数为15°或105°.分析 连OA、OB、OC,求得△AOB是等边三角形,△OBC是等腰直角三角形,从而求得∠ABO=60°,∠OBC=45,即可求得∠ABC的度数.
解答  解:连OA、OB、OC,
解:连OA、OB、OC,
∵⊙O的直径为2,
∴OA=OB=OC=1,
∵AB=1,
∴OA=OB=AB,
∴△AOB是等边三角形,
∴∠ABO=60°,
∵OB=OC=1,BC=$\sqrt{2}$,
∴OB2+OC2=BC2,
∴△OBC是等腰直角三角形,
∴∠OBC=45°,
∴∠ABC的度数为60°-45°=15°或60°+45°=105°;
故答案为15°或105°.
点评 本题考查了等边三角形的判定和性质,直角三角形的判定和性质,作出辅助线构建等边三角形和直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若x3=-8,则x的值是( )
| A. | x=-2 | B. | x=2 | C. | x=±2 | D. | 以上都可以 |
3.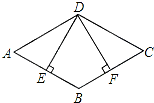 如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
 如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.
如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为( )cm2.| A. | 16$\sqrt{3}$ | B. | 64 | C. | 8$\sqrt{3}$ | D. | 8 |
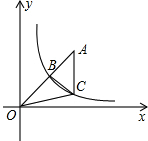 反比例反数y=$\frac{k}{x}$(x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=$\frac{k}{x}$(x>0)的图象于点C,连接BC、OC,S△BOC=3,则k=4.
反比例反数y=$\frac{k}{x}$(x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=$\frac{k}{x}$(x>0)的图象于点C,连接BC、OC,S△BOC=3,则k=4.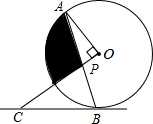 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB. 如图,△ABC中,∠B=2∠C,AD⊥BC于D,M是BC的中点,求证:AB=2DM.
如图,△ABC中,∠B=2∠C,AD⊥BC于D,M是BC的中点,求证:AB=2DM.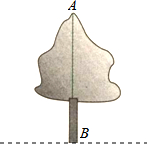 如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由.
如图,要测量树AB的高,可以利用相似三角形的知识,请你设计几种测量方案,并说明每种方案的理由.