题目内容
7．
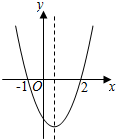二次函数y=ax2+bx+c（a≠0）的大致图象如图所示，关于该二次函数，下列说法不正确的是（ ）| A． | 该函数有最小值 | B． | y随x的增大而减少 | ||
| C． | 对称轴是直线$x=\frac{1}{2}$ | D． | 当-1＜x＜2时，y《＜0 |
分析 根据抛物线的开口方向，利用二次函数的性质判断A；
根据对称轴结合开口方向得出函数的增减性，从而判断B；
根据图形直接判断C；
根据图象，当-1＜x＜2时，抛物线落在x轴的下方，则y＜0，进而判断D．
解答 解：A、由抛物线的开口向上，可知a＞0，函数有最小值，正确，故A选项不符合题意；
B、因为a＞0，所以，在对称轴的左侧，y随x的增大而减小，在对称轴的右侧，y随x的增大而增大，错误，故B选项符合题意；
C、∵抛物线与x轴的交点坐标为（-1，0）、（2，0），
∴抛物线的对称轴为直线x=$\frac{1}{2}$，正确，故C选项不符合题意．
D、由图象可知，当-1＜x＜2时，y＜0，错误，故D选项不符合题意；
故选：B．
点评 本题考查了二次函数的图象：y=ax2+bx+c的图象为抛物线，可利用列表、描点、连线画出二次函数的图象．也考查了二次函数的性质．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
二次函数y=ax2+bx+c（a≠0）的图象如图所示，根据图象写出一条此函数的性质对称轴为直线x=1（答案不唯一）．
12．如果等腰三角形的面积为10，底边长为x，底边上的高为y，则y与x的函数关系式为（ ）
| A． | y=$\frac{10}{x}$ | B． | y=$\frac{5}{x}$ | C． | y=$\frac{20}{x}$ | D． | y=$\frac{x}{20}$ |
16．
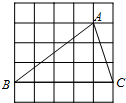如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tan∠ABC的值为（ ）
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tan∠ABC的值为（ ）| A． | 1 | B． | $\frac{3}{5}$ | C． | $\frac{{\sqrt{10}}}{5}$ | D． | $\frac{3}{4}$ |