题目内容
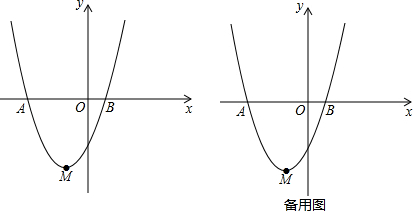
7. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象写出一条此函数的性质对称轴为直线x=1(答案不唯一).
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象写出一条此函数的性质对称轴为直线x=1(答案不唯一).
分析 根据图象结合二次函数的性质即可求解.
解答 解:由图象可知,二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=1;
开口向下;
与x轴交于点(-1,0),(3,0);
当x<1时,y随x的增大而增大;x>1时,y随x的增大而减小.
故答案为:对称轴为直线x=1(答案不唯一).
点评 本题考查了二次函数的性质,二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴是直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-$\frac{b}{2a}$时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.③抛物线y=ax2+bx+c(a≠0)的图象可由抛物线y=ax2的图象向右或向左平移|$\frac{b}{2a}$|个单位,再向上或向下平移|$\frac{4ac-{b}^{2}}{4a}$|个单位得到的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列各式中,正确的是( )
| A. | $\frac{x^6}{x^2}={x^3}$ | B. | $\frac{x+m}{x+n}=\frac{m}{n}$ | C. | $\frac{-a+b}{c}=-\frac{a+b}{c}$ | D. | $\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}$ |
2. 如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
 如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )| A. | 点A与点C | B. | 点A与点D | C. | 点B与点C | D. | 点B与点D |
7.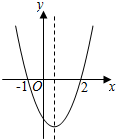 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )| A. | 该函数有最小值 | B. | y随x的增大而减少 | ||
| C. | 对称轴是直线$x=\frac{1}{2}$ | D. | 当-1<x<2时,y《<0 |
 如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.
如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.