题目内容
18.请阅读下面材料,并回答所提出的问题.三角形内角平分线定理:三角形的内角平分线分队边所得的两条线段和这个角的两边对应成比例.
已知:$\frac{AB}{AC}$=$\frac{BD}{DC}$
证明:过C作CE∥DA,交BA的延长线于E.
∴∠1=∠E,∠2=∠3.----①
∵AD是角平分线,
∴∠1=∠2.
∴∠3=∠E.----②
又∵AD∥CE,
∴$\frac{AB}{AE}$=$\frac{BD}{DC}$----③
∴$\frac{AB}{AC}$=$\frac{BD}{DC}$.
(1)上述证明过程中,步骤①②③处的理由是什么?(写出两条即可)
(2)用三角形内角平分线定理解答,已知,△ABC中,AD是角平分线,AB=7cm,AC=4cm,BC=6cm,求BD的长;
(3)我们知道如果两个三角形的高相等,那么它们面积的比就等于底的比.请你通过研究△ABBD和△ACD面积的比来证明三角形内角平分线定理.
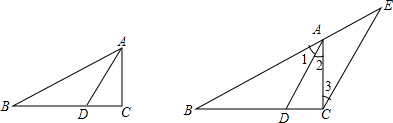
分析 (1)由比例式$\frac{AB}{AE}$=$\frac{BD}{DC}$,想到作平行线,用到了平行线的性质定理;只要证明AE=AC即可,用到了等腰三角形的判定定理;由CE∥AD,写出比例式$\frac{AB}{AC}$=$\frac{BD}{DC}$,用到了平行线分线段成比例定理(推论);
(2)利用三角形内角平分线性质定理,列出比例式,代入数据计算出结果.
(3)根据三角形的面积公式进行证明即可.
解答 解:(1)证明过程中用到的定理有:
①平行线的性质定理;
②等腰三角形的判定定理;
③平行线分线段成比例定理;
(2)∵AD是角平分线,
∴$\frac{BD}{DC}=\frac{AB}{AC}$,
又∵AB=7cm,AC=4cm,BC=6cm,
∴$\frac{BD}{6-BD}=\frac{7}{4}$,
∴BD=$\frac{42}{11}$(cm).
(3)∵△ABD和△ACD的高相等,
可得:△ABD和△ACD面积的比=$\frac{\frac{1}{2}BD×h}{\frac{1}{2}DC×h}=\frac{BD}{DC}$=$\frac{\frac{1}{2}AB×h}{\frac{1}{2}AC×h}=\frac{AB}{AC}$,
可得:$\frac{BD}{DC}=\frac{AB}{AC}$.
点评 此题是一道材料题,根据材料推得的结果进行解题,主要考查平行线分线段成比例定理的理解及运用.

练习册系列答案
相关题目
3.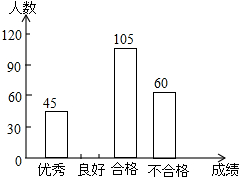 为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:
为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:
请结合图表所给出的信息解答下列问题:
(1)该校初二学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
 为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:
为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
(1)该校初二学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
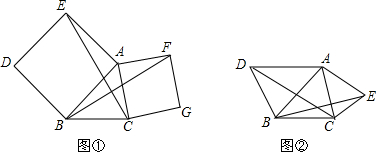
10.如图1,已知三角形纸片ABC,AB=AC,∠C=65°.将其折叠,如图2,使点A与点B重合,折痕为ED,点E,D分别在AB,AC上,那么∠DBC的度数为( )


| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
7.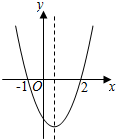 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )| A. | 该函数有最小值 | B. | y随x的增大而减少 | ||
| C. | 对称轴是直线$x=\frac{1}{2}$ | D. | 当-1<x<2时,y《<0 |
 ,实际车牌号为100968.
,实际车牌号为100968. 党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中: