题目内容
2.如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).(1)求线段GF的长;(用含x的代数式表示)
(2)当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?
(3)试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由.
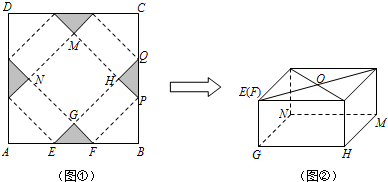
分析 (1)AE=BF=x,据此即可利用x表示出等腰直角△EFG的斜边EF的长,然后利用三角函数求得GF的长;
(2)首先利用矩形的面积公式表示出面积S,然后利用二次函数的性质即可求解;
(3)首先求得与正方形各边相切的线段的长度,然后判断高小于或等于10cm即可判断,然后根据NG的长不小于30cm,高不小于10cm即可列不等式求得x的范围.
解答 解:(1)∵AE=BF=x,
∴EF=AB-AE-BF=60-2x.
∴在Rt△GEF中,GF=$\frac{\sqrt{2}}{2}$EF=$\frac{\sqrt{2}}{2}$×(60-2x)=30$\sqrt{2}$-$\sqrt{2}$x;
(2)∵NG=$\sqrt{2}$AE=$\sqrt{2}$x,即GH=NG=$\sqrt{2}$x,
∴S=$\sqrt{2}$x (30$\sqrt{2}$-$\sqrt{2}$x)=-2x2+60x
=-2(x-15)2+450;
∵-2<0,
∴当x=15时,S最大=450;
(3)能放下.
理由是:当圆柱形工艺品与GHMN相切时,x=15$\sqrt{2}$,
此时,30$\sqrt{2}$-$\sqrt{2}$x=30$\sqrt{2}$-15$\sqrt{2}$×$\sqrt{2}$=30$\sqrt{2}$-30>10,故一定能放下.
根据题意得:$\left\{\begin{array}{l}{30\sqrt{2}-\sqrt{2}x≥10}\\{\sqrt{2}x≥30}\end{array}\right.$
解得:15$\sqrt{2}$≤x≤30-5$\sqrt{2}$.
点评 本题考查了图形的折叠以及 等腰直角三角形的性质,本题中利用x表示出三角形的面积是本题的关键.

 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )
如图,数轴上有A,B,C,D四个点,其中互为相反数的数对应的点是( )| A. | 点A与点C | B. | 点A与点D | C. | 点B与点C | D. | 点B与点D |

| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
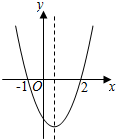 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )| A. | 该函数有最小值 | B. | y随x的增大而减少 | ||
| C. | 对称轴是直线$x=\frac{1}{2}$ | D. | 当-1<x<2时,y《<0 |
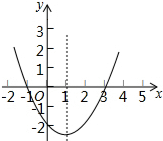 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 当-1<x<3时,y>0 | ||
| C. | 当x<1时,y随x的增大而减小 | D. | 对称轴是直线x=1 |
 ,实际车牌号为100968.
,实际车牌号为100968.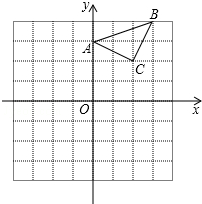 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度). 如图,在△ABC中,AB=AC,AM是外角∠DAC的平分线.
如图,在△ABC中,AB=AC,AM是外角∠DAC的平分线.