题目内容
5.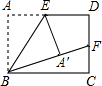 如图,在长方形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD的长度为( )
如图,在长方形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD的长度为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 连接EF,则可证明△EA′F≌△EDF,从而根据BF=BA′+A′F,得出BF的长,在Rt△BCF中,利用勾股定理可求出BC,即得AD的长度.
解答 解:如图所示:连接EF.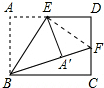
∵点E、点F是AD、DC的中点,
∴AE=ED,CF=DF=$\frac{1}{2}$CD=$\frac{1}{2}$AB=$\frac{1}{2}$.
由折叠的性质可得AE=A′E,
∴A′E=DE,
在Rt△EA′F和Rt△EDF中,$\left\{\begin{array}{l}{EA′=ED}\\{EF=EF}\end{array}\right.$,
∴Rt△EA′F≌Rt△EDF(HL).
∴A′F=DF=$\frac{1}{2}$.
∴BF=BA′+A′F=AB+DF=1+$\frac{1}{2}$=$\frac{3}{2}$.
在Rt△BCF中,BC=$\sqrt{B{F}^{2}{-FC}^{2}}$=$\sqrt{2}$.
∴AD=BC=$\sqrt{2}$.
故选:C.
点评 本题考查了翻折变换的知识,解答本题的关键是连接EF,证明Rt△EA′F≌Rt△EDF,得出BF的长,注意掌握勾股定理的表达式.

练习册系列答案
相关题目
16. 如图所示,已知AB=CD,AD=BC,则图中的全等三角形共有( )
如图所示,已知AB=CD,AD=BC,则图中的全等三角形共有( )
 如图所示,已知AB=CD,AD=BC,则图中的全等三角形共有( )
如图所示,已知AB=CD,AD=BC,则图中的全等三角形共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
14.某家庭农场种植了草莓,每年6月份采集上市.如图,若毎筐草莓以5千克为基准,超过的千克数记为正数,不足的千克数记为负数,记录如图,则这4框草莓的总质量是( )


| A. | 19.7千克 | B. | 19.9千克 | C. | 20.1千克 | D. | 20.3千克 |
 如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为20°.
如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为20°.