题目内容
10．先化简，再求值：[（x+3y）2-（x+y）（x-y）]÷2y，其中x=$\frac{1}{3}$，y=$\frac{1}{5}$．分析 先算乘法，再合并同类项，算除法，最后代入求出即可．
解答 解：[（x+3y）2-（x+y）（x-y）]÷2y
=[x2+6xy+9y2-x2+y2]÷2y
=（6xy+10y2）÷2y
=3x+5y，
当x=$\frac{1}{3}$，y=$\frac{1}{5}$时，原式=3×$\frac{1}{3}$+5×$\frac{1}{5}$=2．
点评 本题考查了整式的混合运算和求值的应用，能正确根据整式的运算法则进行化简是解此题的关键．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
路程s与时间t的图象如图所示，则速度v与时间t的图象为（ ）
18．
如图，从直径是4米的圆形铁皮上剪出一个圆心角是90°的扇形ABC（A、B、C三点在⊙O上），将剪下来的扇形围成一个圆锥的侧面，则该圆锥的底面圆的半径是$\frac{\sqrt{2}}{2}$米．
如图，从直径是4米的圆形铁皮上剪出一个圆心角是90°的扇形ABC（A、B、C三点在⊙O上），将剪下来的扇形围成一个圆锥的侧面，则该圆锥的底面圆的半径是$\frac{\sqrt{2}}{2}$米．
5．
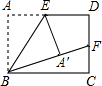如图，在长方形ABCD中，AB=1，E、F分别为AD、CD的中点，沿BE将△ABE折叠，若点A恰好落在BF上，则AD的长度为（ ）
如图，在长方形ABCD中，AB=1，E、F分别为AD、CD的中点，沿BE将△ABE折叠，若点A恰好落在BF上，则AD的长度为（ ）| A． | $\frac{3}{2}$ | B． | 2 | C． | $\sqrt{2}$ | D． | 2$\sqrt{2}$ |
2．小明同学在用描点法画二次函数y=ax2+bx+c图象时，由于粗心，他算错了一个y值，列出了下面表格：
（1）请指出这个错误的y值，并说明理由；
（2）若点M（m，y1），N（m+4，y2）在二次函数y=ax2+bx+c图象上，且m＞-1，试比较y1与y2的大小．
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y=ax2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
（2）若点M（m，y1），N（m+4，y2）在二次函数y=ax2+bx+c图象上，且m＞-1，试比较y1与y2的大小．