题目内容
20．
如图，Rt△ABC中，∠ACB=90°，∠A=55°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB的度数为20°．
分析 根据Rt△ABC中，∠ACB=90°，∠A=55°，将其折叠，使点A落在边CB上A′处，折痕为CD，可以得到∠B的度数，得到∠A与∠CA′D的关系，从而可以得到∠A′DB的度数．
解答 解：∵Rt△ABC中，∠ACB=90°，∠A=55°，将其折叠，使点A落在边CB上A′处，折痕为CD，
∴∠B=90°-∠A=90°-55°=35°，∠A=∠CA′D，
∵∠CA′D=∠B+∠A′DB，
∴55°=35°+∠A′DB，
∴∠A′DB=20°．
故答案为：20°．
点评 本题考查翻折变换，解题的关键是明确题意，知道翻折后的对应角相等，利用数形结合的思想解答问题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．
15．
如图，弦AB⊥OC，垂足为点C，连接OA，若OC=4，AB=6，则sinA等于（ ）
如图，弦AB⊥OC，垂足为点C，连接OA，若OC=4，AB=6，则sinA等于（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{4}{5}$ | D． | $\frac{3}{5}$ |
5．
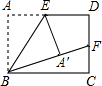如图，在长方形ABCD中，AB=1，E、F分别为AD、CD的中点，沿BE将△ABE折叠，若点A恰好落在BF上，则AD的长度为（ ）
如图，在长方形ABCD中，AB=1，E、F分别为AD、CD的中点，沿BE将△ABE折叠，若点A恰好落在BF上，则AD的长度为（ ）| A． | $\frac{3}{2}$ | B． | 2 | C． | $\sqrt{2}$ | D． | 2$\sqrt{2}$ |