题目内容
13.春节前夕,便民超市把一批进价为每件12元的商品,以每件定价20元销售,每天能售出240件.销售一段时间后发现:如果每件涨价1元,那么每天就少售20件;如果每件降价1元,那么每天能多售出40件.(A)在降价的情况下,要使该商品每天的销售盈利为1800元,每件应降价多少元?
(B)为了使该商品每天销售盈利为1980元,每件定价多少元?
分析 (1)分别表示出每件销售的利润和销售量,根据单件销售利润×销售量=1800列出方程即可求解;
(2)首先根据题意列出方程,利用根的判别式判断方程没有实数根后再列出方程求解即可.
解答 解:(A)设每件应降价x元,根据题意得:(20-x-12)(240+40x)=1800,
解得:x=3或x=-1(舍).
答:每件应降价3元;
(B)①设每件应降价x元,
(20-x-12)(240+40x)=1980,
∵△<0,
∴原方程无实数根;
②设每件应该涨价y元,
(20+y-12)(240-40y)=1980,
解得:y=3或y=1,
则20+3=23元,
20+1=21元,
答:为了使得该商品每天盈利1980元,每件定价应为21或23元.
点评 本题考查了一元二次方程的应用,解题的关键是能够分别表示出销售量和单件的销售利润,从而列出方程求解,解答过程中注意舍去不符合题意的根.

练习册系列答案
相关题目
4. 如图,四边形ABCD内接于⊙O,若∠BOD=100°,则∠DCB的度数为( )
如图,四边形ABCD内接于⊙O,若∠BOD=100°,则∠DCB的度数为( )
 如图,四边形ABCD内接于⊙O,若∠BOD=100°,则∠DCB的度数为( )
如图,四边形ABCD内接于⊙O,若∠BOD=100°,则∠DCB的度数为( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
18. 如图,从直径是4米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A、B、C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是$\frac{\sqrt{2}}{2}$米.
如图,从直径是4米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A、B、C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是$\frac{\sqrt{2}}{2}$米.
 如图,从直径是4米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A、B、C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是$\frac{\sqrt{2}}{2}$米.
如图,从直径是4米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A、B、C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径是$\frac{\sqrt{2}}{2}$米.
5.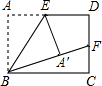 如图,在长方形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD的长度为( )
如图,在长方形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD的长度为( )
 如图,在长方形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD的长度为( )
如图,在长方形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD的长度为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
2.小明同学在用描点法画二次函数y=ax2+bx+c图象时,由于粗心,他算错了一个y值,列出了下面表格:
(1)请指出这个错误的y值,并说明理由;
(2)若点M(m,y1),N(m+4,y2)在二次函数y=ax2+bx+c图象上,且m>-1,试比较y1与y2的大小.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y=ax2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
(2)若点M(m,y1),N(m+4,y2)在二次函数y=ax2+bx+c图象上,且m>-1,试比较y1与y2的大小.