Question

已知一副三角板ABE与ACD．
（1）将两个三角板如图（1）放置，连结BD，计算∠1+∠2=

 

．

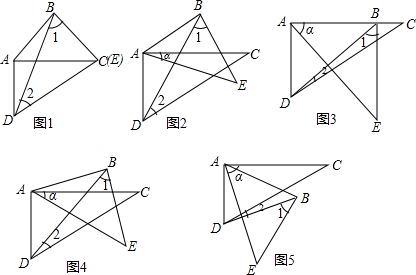
（2）将图（1）中的三角板BAE绕点A顺时针旋转一个锐角α
?当α=

 

时，AB∥CD，如图（2）并计算α+∠1+∠2=

 

．
?当α=45°时，如图（3），计算α+∠1+∠2=

 

．
?在旋转的过程中，当B点在直线CD的上方时，如图（4），α、∠1、∠2间的数量关系是否会发生变化，为什么？
?当B点运动到直线CD的下方时，如图（5）α（∠CAE）、∠1、∠2间的数量关系是否会发生变化，试说明你的结论？

Answer 1

考点：三角形内角和定理,三角形的外角性质

专题：

分析：（1）求出∠BCD，再根据三角形的面积列式计算即可得解；
（2）①根据两直线平行，内错角相等可得∠BAC=∠C，再根据α=∠BAE-∠BAC计算即可得解，再根据三角形的一个外角等于与它不相邻的两个内角的和与三角形的内角和定理列式计算即可得解；
②③④分别根据三角形的一个外角等于与它不相邻的两个内角的和与三角形的内角和定理列式计算即可得解．

解答：解：（1）由题意可知．
Rt△ABE为等腰直角三角形，Rt△ADC为含有60°角的直角三角形，
∠BCD=∠BCA+∠DCA=45°+30°=75°，
所以，∠1+∠2=180°-∠BCD=105°；
故答案是：105°；

（2）①∠1+∠2=105°．
如图2，（∠1+∠E）+（∠α+∠C）+∠2=180°，
∠1+45°+∠α+30°+∠2=180°，
所以，α+∠1+∠2=105°；
②如图3，（∠1+∠2）+（∠α+∠C）+∠E=180°，
∠1+∠2+∠α+30°+45°=180°，
所以，α+∠1+∠2=105°；
③（∠1+∠2）+（∠α+∠C）+∠E=180°，
∠1+∠2+∠α+30°+45°=180°，
所以，α+∠1+∠2=105°；
④∠1+（∠α+∠C-∠2）+∠E=180°，
∠1+∠α+30°-∠2+45°=180°，
所以，∠α+∠1-∠2=105°．
故答案为：（1）105°；（2）15°，α+∠1+∠2=105°，105°．

点评：本题主要考查对三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，能熟练地运用这些性质进行计算并准确识图是解题的关键．