题目内容
2.一次函数y=-x+4图象与x轴、y轴分别交于点A、点B,点P为正比例函数y=kx(k>0)图象上一动点,且满足∠PBO=∠POA,则AP的最小值为2$\sqrt{5}$-2.分析 先依据条件∠PBO=∠POA,得到点P的运动轨迹为y轴右侧以BO为直径的半圆,再根据AP+CP≥AC,可得当点C、P、A三点共线时,AP有最小值,最后根据AP=AC-CP进行计算即可得到AP的最小值.
解答 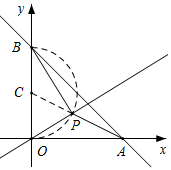 解:如图所示,∵∠POA+∠POB=90°,∠PBO=∠POA,
解:如图所示,∵∠POA+∠POB=90°,∠PBO=∠POA,
∴∠PBO+∠POB=90°,
∴∠BPO=90°,即BP垂直于直线y=kx(k>0),
∴点P的运动轨迹为y轴右侧以BO为直径的半圆,
∵一次函数y=-x+4图象与x轴、y轴分别交于点A、点B,
∴A(4,0),B(0,4),
∴圆心C(0,2),
即AO=4,CO=2,
连接CP,AC,则CP=CO=2,AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵AP+CP≥AC,
∴当点C、P、A三点共线时,AP有最小值,
此时,AP=AC-CP=2$\sqrt{5}$-2,
故答案为:2$\sqrt{5}$-2.
点评 本题主要考查了一次函数图象上点的坐标特征,解决问题的关键是判断点P的运动轨迹为y轴右侧以BO为直径的半圆,依据两点之间,线段最短进行求解.

练习册系列答案
相关题目
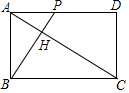 如图,已知矩形ABCD中,AB=2,AD=2$\sqrt{3}$,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①点H不可能在矩形ABCD之外;②AH的最小值为$\sqrt{7}$-$\sqrt{3}$;③在运动过程中,BP扫过的面积始终等于CH扫过的面积;④在运动过程中,点H的运动路线(轨迹)长为$\frac{2}{3}$$\sqrt{3}$π,正确的有(填序号)①②④.
如图,已知矩形ABCD中,AB=2,AD=2$\sqrt{3}$,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①点H不可能在矩形ABCD之外;②AH的最小值为$\sqrt{7}$-$\sqrt{3}$;③在运动过程中,BP扫过的面积始终等于CH扫过的面积;④在运动过程中,点H的运动路线(轨迹)长为$\frac{2}{3}$$\sqrt{3}$π,正确的有(填序号)①②④.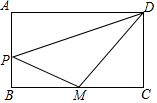 如图.长方形ABCD长为10厘米,宽为6厘米,M为BC的中点,三角形PMD面积为25平方厘米.那么三角形APD的面积为多少平方厘米?
如图.长方形ABCD长为10厘米,宽为6厘米,M为BC的中点,三角形PMD面积为25平方厘米.那么三角形APD的面积为多少平方厘米?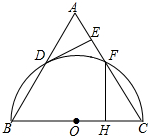 如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.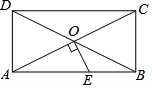 如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E.若BC=4,△AOE的面积为5,则BE=3.
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E.若BC=4,△AOE的面积为5,则BE=3.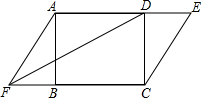 如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.
如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.