题目内容
3.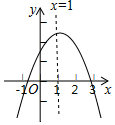 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的交点(x1,0),(x2,0),且-1<x1<0<x2,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则b2=4a(c-n),其中正确的结论有( )个.
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的交点(x1,0),(x2,0),且-1<x1<0<x2,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则b2=4a(c-n),其中正确的结论有( )个.| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 由抛物线的开口方向、对称轴及抛物线与y轴的交点可判断①;由x=-1时函数值y<0可判断②;由当x=1时,函数取得最大值可判断③;由x=-1时,y=a-b+c<0且a=-$\frac{b}{2}$可判断④;由顶点的纵坐标n=$\frac{4ac-{b}^{2}}{4a}$可判断⑤.
解答 解:∵抛物线开口向下,且与y轴的交点在正半轴,
∴a<0,c>0,
∵对称轴x=-$\frac{b}{2a}$=1,
∴b=-2a>0,
∴abc<0,故①正确;
由图象知,x=-1时,y=a-b+c<0,
∴b>a+c,故②正确;
∵当x=1时,函数取得最大值,
∴y=a+b+c>ak2+bk+c(k≠1),
即a+b>k(ka+b)(k为常数,且k≠1),故③正确;
∵x=-1时,y=a-b+c<0,且b=-2a,
∴-$\frac{3}{2}$b+c<0,即2c<3b,故④正确;
∵抛物线顶点坐标为(1,n),
∴n=$\frac{4ac-{b}^{2}}{4a}$,即b2=4a(c-n),故⑤正确;
故选:A.
点评 本题主要考查二次函数的图象与系数的关系,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
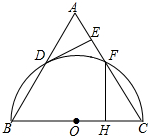 如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.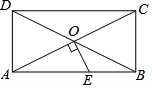 如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E.若BC=4,△AOE的面积为5,则BE=3.
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E.若BC=4,△AOE的面积为5,则BE=3. 己知A(-1,0),B(2,0),点P是直线y=x+4上的一动点且在x轴上方,如果以点A、B、P、Q为顶点的平行四边形的面积等于6,画出图形并求出点P和点Q的坐标.
己知A(-1,0),B(2,0),点P是直线y=x+4上的一动点且在x轴上方,如果以点A、B、P、Q为顶点的平行四边形的面积等于6,画出图形并求出点P和点Q的坐标.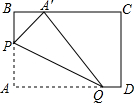 在矩形纸片中,AB=3,AD=5,如图所示.折叠纸片,使点A落在BC边上的点A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则移动过程中线段BA′的长度取值范围是1≤BA'≤3.
在矩形纸片中,AB=3,AD=5,如图所示.折叠纸片,使点A落在BC边上的点A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则移动过程中线段BA′的长度取值范围是1≤BA'≤3.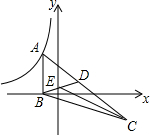 如图,△ABC的顶点A在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AB⊥x轴,垂足为B,顶点C在第四象限,△ABC的中线BD交y轴于点E,连接CE,若△BCE的面积是6,则k的值为-12.
如图,△ABC的顶点A在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AB⊥x轴,垂足为B,顶点C在第四象限,△ABC的中线BD交y轴于点E,连接CE,若△BCE的面积是6,则k的值为-12.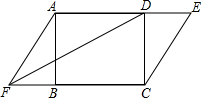 如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.
如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.