题目内容
20.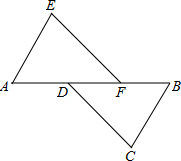 如图,A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.
如图,A,D,F,B在同一直线上,AD=BF,AE=BC,且AE∥BC.(1)求证:△AEF≌△BCD;
(2)连ED,CF,则四边形EDCF是平行四边形(从平行四边形,矩形,菱形,正方形中选填并证明).
分析 (1)根据SAS即可证明△AEF≌△BCD;
(2)结论:平行四边形.只要证明EF=DC.EF∥CD即可;
解答 (1)证明:∵AE∥BC,
∴∠A=∠B,
∵AD=BF,
∴AF=BD,
在△AEF和△BCD中,
$\left\{\begin{array}{l}{AE=BC}\\{∠A=∠B}\\{AF=BD}\end{array}\right.$,
∴△AEF≌△BCD.
(2)结论:四边形DEFC是平行四边形.
证明:连接DE、CF.
∵△AEF≌△BCD,
∴∠AFE=∠BDC,EF=DC,
∴EF∥CD,
∴四边形DEFC是平行四边形,
故答案为:平行四边形.
点评 本题考查全等三角形的判定和性质、平行线的性质和判定、平行四边形的判定等知识,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 某商品四天内每天每斤的进价与售价信息如图所示,则售出这种商品每斤利润最大的是( )
某商品四天内每天每斤的进价与售价信息如图所示,则售出这种商品每斤利润最大的是( )
 某商品四天内每天每斤的进价与售价信息如图所示,则售出这种商品每斤利润最大的是( )
某商品四天内每天每斤的进价与售价信息如图所示,则售出这种商品每斤利润最大的是( )| A. | 第一天 | B. | 第二天 | C. | 第三天 | D. | 第四天 |
10.若一个正比例函数的图象经过A(3,-6),B(m,-4)两点,则m的值为( )
| A. | 2 | B. | 8 | C. | -2 | D. | -8 |
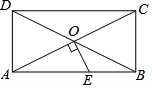 如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E.若BC=4,△AOE的面积为5,则BE=3.
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E.若BC=4,△AOE的面积为5,则BE=3.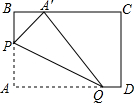 在矩形纸片中,AB=3,AD=5,如图所示.折叠纸片,使点A落在BC边上的点A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则移动过程中线段BA′的长度取值范围是1≤BA'≤3.
在矩形纸片中,AB=3,AD=5,如图所示.折叠纸片,使点A落在BC边上的点A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,则移动过程中线段BA′的长度取值范围是1≤BA'≤3.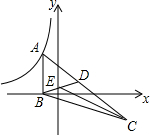 如图,△ABC的顶点A在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AB⊥x轴,垂足为B,顶点C在第四象限,△ABC的中线BD交y轴于点E,连接CE,若△BCE的面积是6,则k的值为-12.
如图,△ABC的顶点A在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AB⊥x轴,垂足为B,顶点C在第四象限,△ABC的中线BD交y轴于点E,连接CE,若△BCE的面积是6,则k的值为-12.
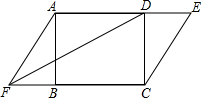 如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.
如图,在矩形ABCD中,若延长AD至点E,延长CB至点F,并使得DE=BF,连接AF、CE及DF.