题目内容
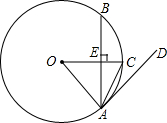 如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若点D在⊙O的外且∠DAC=∠BAC,求证:直线AD是⊙O的切线.
如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若点D在⊙O的外且∠DAC=∠BAC,求证:直线AD是⊙O的切线.考点:切线的判定
专题:证明题
分析:首先得出∠OCA+∠CAE=90°,进而求出∠DAC+∠OAC=90°,即可得出答案.
解答:证明:∵半径OC垂直于弦AB,
∴∠OCA+∠CAE=90°,
∵CO=OA,
∴∠OCA=∠OAC,
∵∠DAC=∠BAC,
∴∠DAC+∠OAC=90°,
∴OA⊥AD,
即直线AD是⊙O的切线.
∴∠OCA+∠CAE=90°,
∵CO=OA,
∴∠OCA=∠OAC,
∵∠DAC=∠BAC,
∴∠DAC+∠OAC=90°,
∴OA⊥AD,
即直线AD是⊙O的切线.
点评:此题主要考查了切线的判定,得出∠DAC+∠OAC=90°是解题关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,AC⊥BC,DE是AB的垂直平分线,∠CAE=20°,则∠B=( )
如图,AC⊥BC,DE是AB的垂直平分线,∠CAE=20°,则∠B=( )| A、30° | B、35° |
| C、40° | D、45° |
 如图,在△ABC中,AD⊥BC于点D,BD=CD,若BC=5,AD=4,则图中阴影部分的面积为( )
如图,在△ABC中,AD⊥BC于点D,BD=CD,若BC=5,AD=4,则图中阴影部分的面积为( )| A、5 | B、10 | C、15 | D、20 |
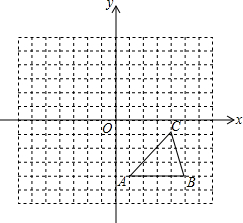 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1). 已知:P为等腰△ABC中底边BC上一点,且PE⊥AB于E,PF⊥AC于F,BH为△ABC的高,猜想:PE、PF和BH之间的数量关系,并加以证明.
已知:P为等腰△ABC中底边BC上一点,且PE⊥AB于E,PF⊥AC于F,BH为△ABC的高,猜想:PE、PF和BH之间的数量关系,并加以证明. 如图,圆O的一条弦AB将圆周长分为3:7两部分,试求弦AB所对的圆心角和圆周角的度数,并作出图.
如图,圆O的一条弦AB将圆周长分为3:7两部分,试求弦AB所对的圆心角和圆周角的度数,并作出图.