题目内容
如图,在正方形ABCD中,E、F分别是BC、DC上的两点,若EF=BE+DF.
(1)求证:∠EAF=45°;
(2)作∠EFC的平分线FG交AE的延长线于G,连接CG,如图2.求证:BC-CF=
CG;
(3)若F是DC的中点,AB=4,如图3,求EG的长.
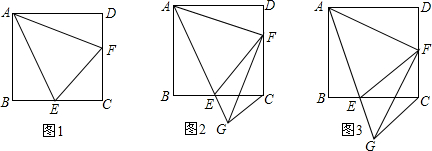
(1)求证:∠EAF=45°;
(2)作∠EFC的平分线FG交AE的延长线于G,连接CG,如图2.求证:BC-CF=
| ||
| 2 |
(3)若F是DC的中点,AB=4,如图3,求EG的长.

考点:四边形综合题
专题:综合题
分析:(1)延长CB至G,使BG=FD,连接AG,如图1,利用“SAS”证明△ABG≌△ADF,得到AG=AF,∠BAG=∠DAF,而EF=BE+DF,所以EF=EG,再根据“SSS”证明∴△AEG≌△AEF,得到∠EAG=∠EAF,则∠EAF=∠DAF+∠ABE,然后利用∠EAF+∠DAF+∠ABE=90°,即可得到∠EAF=45°;
(2)过点G作GH⊥DC于H,如图2,由(1)中∠AEB=∠AEF,根据角平分线定义得到∠EFG=∠CFG,有三角形外角性质得∠BEF=∠EFC+∠ECF,则2∠AEB=2∠EFC+90°,所以∠AEB=∠EFC+45°,而∠AEB=∠EFC+∠EGF,所以∠EGF=45°,于是可判断△FAG为等腰直角三角形,得到FA=FG,∠AFG=90°;接着根据等角的余角相等得到∠DAF=∠HFG,于是可根据“AAS”证明△ADF≌△FHG,得到AD=FH,DF=GH,易得DF=CH=GH,则可判断△CGH为等腰直角三角形,得到CH=
GC,所以DC-CF=DF=
CG,即有BC-CF=
CG;
(3)作GQ⊥BC于Q,GH⊥DC于H,如图3,DF=CF=2,由(2)得CH=GH=2,则CQ=GQ=2,BQ=2,设BE=x,则EF=BE+DF=x+2,EC=4-x,在△CEF中利用勾股定理的(4-x)2+22=(x+2)2,解得x=
,则EQ=BQ-BE=
,然后在Rt△GQE中根据勾股定理可计算出EG.
(2)过点G作GH⊥DC于H,如图2,由(1)中∠AEB=∠AEF,根据角平分线定义得到∠EFG=∠CFG,有三角形外角性质得∠BEF=∠EFC+∠ECF,则2∠AEB=2∠EFC+90°,所以∠AEB=∠EFC+45°,而∠AEB=∠EFC+∠EGF,所以∠EGF=45°,于是可判断△FAG为等腰直角三角形,得到FA=FG,∠AFG=90°;接着根据等角的余角相等得到∠DAF=∠HFG,于是可根据“AAS”证明△ADF≌△FHG,得到AD=FH,DF=GH,易得DF=CH=GH,则可判断△CGH为等腰直角三角形,得到CH=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(3)作GQ⊥BC于Q,GH⊥DC于H,如图3,DF=CF=2,由(2)得CH=GH=2,则CQ=GQ=2,BQ=2,设BE=x,则EF=BE+DF=x+2,EC=4-x,在△CEF中利用勾股定理的(4-x)2+22=(x+2)2,解得x=
| 4 |
| 3 |
| 2 |
| 3 |
解答: (1)证明:延长CB至G,使BG=FD,连接AG,如图1,
(1)证明:延长CB至G,使BG=FD,连接AG,如图1,
∵四边形ABCD为正方形,
∴AB=AD,∠ABC=∠D=90°,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∵EF=BE+DF,
∴EF=EG,
在△AEG和△AEF中,
,
∴△AEG≌△AEF(SSS),
∴∠EAG=∠EAF,
∵∠BAG=∠DAF,
∴∠EAF=∠DAF+∠ABE,
∵∠EAF+∠DAF+∠ABE=90°,
∴∠EAF=45°;
(2)证明:过点G作GH⊥DC于H,如图2,
由(1)中∠AEB=∠AEF,
∵FG平分∠EFC,
∴∠EFG=∠CFG,
∵∠BEF=∠EFC+∠ECF,
∴2∠AEB=2∠EFC+90°,即∠AEB=∠EFC+45°,
而∠AEB=∠EFG+∠EGF,
∴∠EGF=45°,
∵∠GAF=45°,
∴△FAG为等腰直角三角形,
∴FA=FG,∠AFG=90°,
∴∠AFD+∠HFG=90°,
而∠AFD+∠DAF=90°,
∴∠DAF=∠HFG,
在△ADF和△FHG中,
,
∴△ADF≌△FHG(AAS),
∴AD=FH,DF=GH,
而AD=DC,
∴DC=FH,
∴DF=CH=GH,
∴△CGH为等腰直角三角形,
∴CH=
GC,
∴DC-CF=DF=CH=
CG,
∴BC-CF=
CG;
(3)解:作GQ⊥BC于Q,GH⊥DC于H,如图3,
∵F是DC的中点,AB=4,
∴DF=CF=2,
由(2)得CH=GH=2,
∴CQ=GQ=2,
∴BQ=2,
设BE=x,则EF=BE+DF=x+2,EC=4-x,
在△CEF中,∵CE2+CF2=EF2,
∴(4-x)2+22=(x+2)2,
解得x=
,
∴EQ=BQ-BE=2-
=
,
在Rt△GQE中,EG=
=
=
.
 (1)证明:延长CB至G,使BG=FD,连接AG,如图1,
(1)证明:延长CB至G,使BG=FD,连接AG,如图1,∵四边形ABCD为正方形,
∴AB=AD,∠ABC=∠D=90°,
在△ABG和△ADF中,
|
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∵EF=BE+DF,
∴EF=EG,
在△AEG和△AEF中,
|
∴△AEG≌△AEF(SSS),
∴∠EAG=∠EAF,
∵∠BAG=∠DAF,
∴∠EAF=∠DAF+∠ABE,
∵∠EAF+∠DAF+∠ABE=90°,
∴∠EAF=45°;
(2)证明:过点G作GH⊥DC于H,如图2,
由(1)中∠AEB=∠AEF,
∵FG平分∠EFC,

∴∠EFG=∠CFG,
∵∠BEF=∠EFC+∠ECF,
∴2∠AEB=2∠EFC+90°,即∠AEB=∠EFC+45°,
而∠AEB=∠EFG+∠EGF,
∴∠EGF=45°,
∵∠GAF=45°,
∴△FAG为等腰直角三角形,
∴FA=FG,∠AFG=90°,
∴∠AFD+∠HFG=90°,
而∠AFD+∠DAF=90°,
∴∠DAF=∠HFG,
在△ADF和△FHG中,
|
∴△ADF≌△FHG(AAS),
∴AD=FH,DF=GH,
而AD=DC,
∴DC=FH,
∴DF=CH=GH,
∴△CGH为等腰直角三角形,
∴CH=
| ||
| 2 |
∴DC-CF=DF=CH=
| ||
| 2 |
∴BC-CF=
| ||
| 2 |

(3)解:作GQ⊥BC于Q,GH⊥DC于H,如图3,
∵F是DC的中点,AB=4,
∴DF=CF=2,
由(2)得CH=GH=2,
∴CQ=GQ=2,
∴BQ=2,
设BE=x,则EF=BE+DF=x+2,EC=4-x,
在△CEF中,∵CE2+CF2=EF2,
∴(4-x)2+22=(x+2)2,
解得x=
| 4 |
| 3 |
∴EQ=BQ-BE=2-
| 4 |
| 3 |
| 2 |
| 3 |
在Rt△GQE中,EG=
| GQ2+EQ2 |
22+(
|
2
| ||
| 3 |
点评:本题考查了四边形的综合题:熟练掌握正方形的性质、等腰直角三角形的性质;会利用三角形全等解决线段和角相等的问题;能运用勾股定理计算线段的长.

练习册系列答案
相关题目
下列等式不成立的是( )
A、
| ||
| B、(-2)3=-8 | ||
| C、-(-4)=4 | ||
| D、0×2009=2009 |
在函数y=kx(k<0)的图象上有A(1,y1),B(-1,y2),C(-2,y3)三个点,则下列各式正确的是( )
| A、y1<y2<y3 |
| B、y1<y3<y2 |
| C、y3<y2<y1 |
| D、y2<y3<y1 |
 如图,AC平分∠BAD,CE⊥AB于E,BC=CD,∠ADC+∠B=180°,探究2AE与AB,AD的数量关系,并加以证明.
如图,AC平分∠BAD,CE⊥AB于E,BC=CD,∠ADC+∠B=180°,探究2AE与AB,AD的数量关系,并加以证明.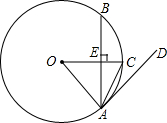 如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若点D在⊙O的外且∠DAC=∠BAC,求证:直线AD是⊙O的切线.
如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若点D在⊙O的外且∠DAC=∠BAC,求证:直线AD是⊙O的切线. 如图:AD是∠CAB的平分线,DE⊥AB,DC⊥AC,若△ACB的面积为150,AB=18,AC=12,则DE的长是
如图:AD是∠CAB的平分线,DE⊥AB,DC⊥AC,若△ACB的面积为150,AB=18,AC=12,则DE的长是