题目内容
 如图,圆O的一条弦AB将圆周长分为3:7两部分,试求弦AB所对的圆心角和圆周角的度数,并作出图.
如图,圆O的一条弦AB将圆周长分为3:7两部分,试求弦AB所对的圆心角和圆周角的度数,并作出图.考点:圆心角、弧、弦的关系,圆周角定理
专题:
分析:求弦所对的圆周角,要分情况考虑:当圆周角在优弧上或在劣弧上.根据圆周角等于它所圆心角的一半即可求解.
解答: 解:根据弦AB分圆周长为3:7两部分,
解:根据弦AB分圆周长为3:7两部分,
所以弦所对的圆心角为108°,
再根据圆周角的度数等于它所对圆心角度数的一半,
得弦对的圆周角分别是54°和126°.
 解:根据弦AB分圆周长为3:7两部分,
解:根据弦AB分圆周长为3:7两部分,所以弦所对的圆心角为108°,
再根据圆周角的度数等于它所对圆心角度数的一半,
得弦对的圆周角分别是54°和126°.
点评:本题考查了圆心角、弧、弦以及圆周角定理,要特别注意弦所对的圆周角应有两种情况.

练习册系列答案
相关题目
下列等式不成立的是( )
A、
| ||
| B、(-2)3=-8 | ||
| C、-(-4)=4 | ||
| D、0×2009=2009 |
在函数y=kx(k<0)的图象上有A(1,y1),B(-1,y2),C(-2,y3)三个点,则下列各式正确的是( )
| A、y1<y2<y3 |
| B、y1<y3<y2 |
| C、y3<y2<y1 |
| D、y2<y3<y1 |
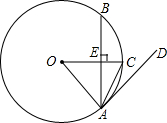 如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若点D在⊙O的外且∠DAC=∠BAC,求证:直线AD是⊙O的切线.
如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若点D在⊙O的外且∠DAC=∠BAC,求证:直线AD是⊙O的切线.