题目内容
 已知:P为等腰△ABC中底边BC上一点,且PE⊥AB于E,PF⊥AC于F,BH为△ABC的高,猜想:PE、PF和BH之间的数量关系,并加以证明.
已知:P为等腰△ABC中底边BC上一点,且PE⊥AB于E,PF⊥AC于F,BH为△ABC的高,猜想:PE、PF和BH之间的数量关系,并加以证明.考点:等腰三角形的性质
专题:
分析:连接AP,根据等腰三角形的性质可表示出S△ABC=S△ABP+S△ACP=
×AC×(PE+PF),同时可表示出S△ABC=
AC×BH,从而可得到PE+PF=BH.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:PE+PF=BH.理由如下:
解:PE+PF=BH.理由如下:
连接AP.
∵AB=AC,
∴S△ABC=S△ABP+S△ACP=
AB×PE+
AC×PF=
×AC×(PE+PF),
∵S△ABC=
AC×BH,
∴PE+PF=BH.
 解:PE+PF=BH.理由如下:
解:PE+PF=BH.理由如下:连接AP.
∵AB=AC,
∴S△ABC=S△ABP+S△ACP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
∴PE+PF=BH.
点评:此题主要考查等腰三角形的性质及三角形面积的综合运用,此题的关键是利用面积公式将所求联系在一起.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
在△ABC中,∠A=∠B=
∠C,则此三角形是( )
| 1 |
| 3 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
下列等式不成立的是( )
A、
| ||
| B、(-2)3=-8 | ||
| C、-(-4)=4 | ||
| D、0×2009=2009 |
 如图,AC平分∠BAD,CE⊥AB于E,BC=CD,∠ADC+∠B=180°,探究2AE与AB,AD的数量关系,并加以证明.
如图,AC平分∠BAD,CE⊥AB于E,BC=CD,∠ADC+∠B=180°,探究2AE与AB,AD的数量关系,并加以证明.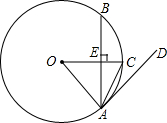 如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若点D在⊙O的外且∠DAC=∠BAC,求证:直线AD是⊙O的切线.
如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若点D在⊙O的外且∠DAC=∠BAC,求证:直线AD是⊙O的切线. 如图:AD是∠CAB的平分线,DE⊥AB,DC⊥AC,若△ACB的面积为150,AB=18,AC=12,则DE的长是
如图:AD是∠CAB的平分线,DE⊥AB,DC⊥AC,若△ACB的面积为150,AB=18,AC=12,则DE的长是