题目内容
8．已知$\sqrt{x-2}$+y2+6y+|z-4|=-9，则2x-y+z=11．分析 首先把原式变为$\sqrt{x-2}$+（y+3）2+|z-4|=0，利用非负数的性质求得x、y、z进一步代入代数式求得答案即可．
解答 解：∵$\sqrt{x-2}$+y2+6y+|z-4|=-9，
∴$\sqrt{x-2}$+（y+3）2+|z-4|=0，
∴x-2=0，y+3=0，z-4=0，
解得：x=2，y=-3，z=4，
∴2x-y+z=4+3+4=11．
故答案为：11．
点评 此题考查配方法的运用，非负数的性质，掌握完全平方公式和二次根式、绝对值的意义是解决问题的关键．
练习册系列答案
名题金卷系列答案
相关题目
19．下列计算正确的是（ ）
| A． | $\sqrt{8^2}$=±8 | B． | $\frac{{\sqrt{8}}}{{\sqrt{3}}}=\frac{2}{3}\sqrt{6}$ | C． | 4$\sqrt{2}-3\sqrt{2}$=1 | D． | $\sqrt{12}×\sqrt{\frac{1}{3}}=4$ |
16．为了比较甲、乙两块地的小麦哪块长得更整齐，应选择的统计量为（ ）
| A． | 平均数 | B． | 中位数 | C． | 众数 | D． | 方差 |
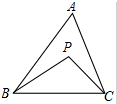如图，在△ABC中，∠ABP=2∠PBC，∠ACP=2∠PCB．
随着房价的上涨，某开房商调研发现大多数人无力购买面积较大的房子，该开发商决定建造一批“经济适用房”．如图是一套小户型“经济适用房”的平面尺寸图．