题目内容
18.已知a、b满足|a2+b2-8|+(a-b-1)2=0.(1)求ab的值;
(2)先化简,再求值:(2a-b+1)(2a-b-1)-(a+2b)(a-b).
分析 (1)根据绝对值和偶次方的非负性求出a2+b2=8,a-b=1,再根据完全平方公式进行求出ab;
(2)先算乘法,再合并同类项,最后整体代入求出即可.
解答 解:(1)∵|a2+b2-8|+(a-b-1)2=0,
∴a2+b2-8=0,a-b-1=0,
∴a2+b2=8,a-b=1,
∴(a-b)2=1,
∴a2+b2-2ab=1,
∴8-2ab=1,
∴ab=$\frac{7}{2}$;
(2)(2a-b+1)(2a-b-1)-(a+2b)(a-b)
=(2a-b)2-12-(a2-ab+2ab-2b2)
=4a2-4ab+b2-1-a2+ab-2ab+2b2
=3a2+3b2-5ab-1
=3(a2+b2)-5ab-1,
当a2+b2=8,ab=$\frac{7}{2}$时,原式=3×8-5×$\frac{7}{2}$-1=$\frac{11}{2}$.
点评 本题考查了绝对值,偶次方,乘法公式的应用,也考查了整式的混合运算和求值的应用,能正确运用整式的运算法则进行计算和化简是解此题的关键.

练习册系列答案
相关题目
9.下列各数中,无理数的个数有( )
-0.2020020002,$\sqrt{2}$,$\frac{1}{2}$,$\frac{π}{2}$,-$\sqrt{4}$,$\frac{2}{3}$.
-0.2020020002,$\sqrt{2}$,$\frac{1}{2}$,$\frac{π}{2}$,-$\sqrt{4}$,$\frac{2}{3}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.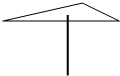 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )| A. | 三边高的交点 | B. | 三条角平分线的交点 | ||
| C. | 三边垂直平分线的交点 | D. | 三边中线的交点 |
13.将长为40cm,宽为15cm的长方形白纸,按图所示的方法粘合起来,粘合部分宽为5cm.

(1)根据上图,将表格补充完整.
(2)设x张白纸粘合后的总长度为ycm,则y与x之间的关系式是什么?
(3)你认为多少张白纸粘合起来总长度可能为2015cm吗?为什么?

(1)根据上图,将表格补充完整.
| 白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
| 纸条长度 | 40 | 75 | 110 | 145 | 180 | … |
(3)你认为多少张白纸粘合起来总长度可能为2015cm吗?为什么?
10.下列命题中,假命题是( )
| A. | 有两条边对应相等的两个直角三角形全等 | |
| B. | 有两条边和一个叫对应相等的两个三角形全等 | |
| C. | 在同一平面内,垂直于同一直线的两条直线互相平行 | |
| D. | 三角形中至少有一个角大于60° |