题目内容
3.已知${x^{{k^2}-2}}-$$\sqrt{1-k}x+\frac{1}{2}$=0是关于x的一元二次方程,则k为-2.分析 根据一元二次方程:未知数的最高次数是2;二次项系数不为0;是整式方程;含有一个未知数,可得答案.
解答 解:由${x^{{k^2}-2}}-$$\sqrt{1-k}x+\frac{1}{2}$=0是关于x的一元二次方程,得
k2-2=2,且1-k≥0,
解得k=-2,
故答案为:-2.
点评 本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.

练习册系列答案
相关题目
13.将长为40cm,宽为15cm的长方形白纸,按图所示的方法粘合起来,粘合部分宽为5cm.

(1)根据上图,将表格补充完整.
(2)设x张白纸粘合后的总长度为ycm,则y与x之间的关系式是什么?
(3)你认为多少张白纸粘合起来总长度可能为2015cm吗?为什么?

(1)根据上图,将表格补充完整.
| 白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
| 纸条长度 | 40 | 75 | 110 | 145 | 180 | … |
(3)你认为多少张白纸粘合起来总长度可能为2015cm吗?为什么?
18.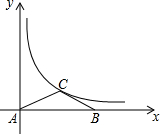 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )| A. | 一直不变 | B. | 先增大后减小 | C. | 先减小后增大 | D. | 先增大后不变 |
15.估算$\sqrt{29}$-2的值( )
| A. | 在1至2之间 | B. | 在2至3之间 | C. | 在3至4之间 | D. | 在4至5之间 |
 如图,线段AC是菱形ABCD的一条对角线,过顶点A、C分别作对角线AC的垂线,交CB、AD的延长线于点E、F.
如图,线段AC是菱形ABCD的一条对角线,过顶点A、C分别作对角线AC的垂线,交CB、AD的延长线于点E、F.