题目内容
2. 如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
分析 过点A作AH⊥第一、三象限的角平分线于点M,作MN⊥x轴于N,如图,根据垂线段最短可判断点B在点H时,AB最短,然后根据等腰直角三角形的性质求出MN和ON的长可确定H点的坐标,从而得到满足条件的B点坐标.
解答 解:过点A作AH⊥第一、三象限的角平分线于点M,作MN⊥x轴于N,如图,
∵∠AOM=45°,
∴△AOM为等腰直角三角形,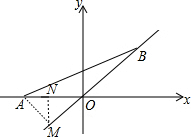
∴MN=ON=AN=$\frac{1}{2}$,
∴H(-$\frac{1}{2}$,-$\frac{1}{2}$),
∴当线段AB最短时,点B的坐标为(-$\frac{1}{2}$,-$\frac{1}{2}$).
故选C.
点评 本题考查了坐标与图形性质:利用点的坐标特征计算线段的长和判断线段与坐标轴的位置关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知关于x的不等式$\frac{4x+a}{3}$>1的解都是不等式$\frac{2x+1}{3}$>0的解,则a的范围是( )
| A. | a=5 | B. | a≥5 | C. | a≤5 | D. | a<5 |
 把一张长方形纸片如图那样折叠后,B,C两点分别落在点B′,C′处,若∠C′ED=64°,则∠AFE的度数为58°.
把一张长方形纸片如图那样折叠后,B,C两点分别落在点B′,C′处,若∠C′ED=64°,则∠AFE的度数为58°. 如图,在△ABC中,D是BC边上一点,且BA=BD,∠DAC=$\frac{1}{2}$∠B,∠C=50°.求∠BAC的度数.
如图,在△ABC中,D是BC边上一点,且BA=BD,∠DAC=$\frac{1}{2}$∠B,∠C=50°.求∠BAC的度数. 如图,在⊙O中,弦AB、DC的延长线交于点E,且DC=CE,C是$\widehat{BD}$的中点.求证:AD是⊙O的直径.
如图,在⊙O中,弦AB、DC的延长线交于点E,且DC=CE,C是$\widehat{BD}$的中点.求证:AD是⊙O的直径.