题目内容
13.直线l1:y=$\frac{2}{3}$x+$\frac{1-a}{3}$与直线l2:y=-$\frac{1}{2}$x+a的交点在第二象限内,则a的取值范围是-$\frac{1}{3}$<a<$\frac{1}{4}$.分析 联立方程,求交点坐标,根据交点在第二象限,建立不等式,可求得a的取值范围.
解答 解:联立方程,由$\frac{2}{3}x+\frac{1-a}{3}$=$-\frac{1}{2}x+a$,可得x=$\frac{8a-2}{7}$,
∴y=$-\frac{1}{2}x+a$=$\frac{8a-2}{7}$,
∵交点在第二象限内,
∴$\frac{8a-2}{7}$<0,且$\frac{1+3a}{7}$>0,
∴-$\frac{1}{3}$$<a<\frac{1}{4}$,
故答案为:$-\frac{1}{3}<a<\frac{1}{4}$.
点评 本题考查直线的交点,考查解不等式,正确求交点坐标是关键.

练习册系列答案
相关题目
8.王刚同学在解关于x的方程x2-3x+c=0时,误将-3x看作+3x,结果解得x1=1 x2=-4,则原方程的解为( )
| A. | x1=-1 x2=-4 | B. | x1=1 x2=4 | C. | x1=-1 x2=4 | D. | x1=2 x2=3 |
2. 如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
 如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
3.已知a>b>c,设M=$\frac{2}{a-c}$,N=$\frac{1}{a-b}$-$\frac{1}{b-c}$,则M与N的大小关系为( )
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
 如图,在长方形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在线段AC上的点E、F处,折痕分别为CM、AN.
如图,在长方形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在线段AC上的点E、F处,折痕分别为CM、AN. 把如图所示的长方形切一刀,再拼成一个平行四边形,画出切割线与拼接图.
把如图所示的长方形切一刀,再拼成一个平行四边形,画出切割线与拼接图.
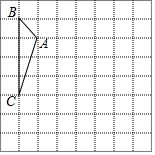 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求解决下列问题:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求解决下列问题: