题目内容
14.已知关于x的不等式$\frac{4x+a}{3}$>1的解都是不等式$\frac{2x+1}{3}$>0的解,则a的范围是( )| A. | a=5 | B. | a≥5 | C. | a≤5 | D. | a<5 |
分析 先把a看作常数求出两个不等式的解集,再根据同大取大列出不等式求解即可.
解答 解:由$\frac{4x+a}{3}$>1得,x>$\frac{3-a}{4}$,
由$\frac{2x+1}{3}$>0得,x>-$\frac{1}{2}$,
∵关于x的不等式$\frac{4x+a}{3}$>1的解都是不等式$\frac{2x+1}{3}$>0的解,
∴$\frac{3-a}{4}$≥-$\frac{1}{2}$,
解得a≤5.
即a的取值范围是:a≤5.
故选C.
点评 本题考查了不等式的解集,解一元一次不等式,分别求出两个不等式的解集,再根据同大取大列出关于a的不等式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
 如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在第一、三象限的角平分线上运动,当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
19.无论x为任何实数,x2-4x+9的取值范围为( )
| A. | x2-4x+9>9 | B. | x2-4x+9≥18 | C. | x2-4x+9≥5 | D. | x2-4x+9≤5 |
3.已知a>b>c,设M=$\frac{2}{a-c}$,N=$\frac{1}{a-b}$-$\frac{1}{b-c}$,则M与N的大小关系为( )
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
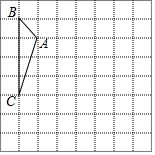 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求解决下列问题:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求解决下列问题: 如图,△ABC的两条角平分线BE,CD相交于点O.
如图,△ABC的两条角平分线BE,CD相交于点O. 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.