题目内容
7．
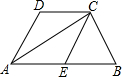已知：如图所示，AB∥CD，AD∥CE，且∠ACB=90°，E为AB的中点．（1）试说明DE与AC互相平分；
（2）探究：当四边形AECD是正方形时，求∠B的度数．
分析 （1）证四边形ADCE是平行四边形，得出DE与AC互相平分即可；
（2）当四边形AECD是正方形时，证出△BCE是等腰Rt△，由此可求出∠B的度数．
解答 （1证明：连接DE，
∵AB∥CD，AD∥CE，
∴四边形AECD是平行四边形，
∴DE与AC互相平分；
（2）解：∵四边形AECD是正方形，
∴CE⊥AB，AE=CE，
∵在Rt△ACB中，E为AB的中点．
∴CE=AE=EB，
∴△BCE是等腰直角三角形，
∴∠B=45°．
点评 本题考查了平行四边形的判定、正方形的性质、等腰直角三角形的判定与性质；熟练掌握平行四边形的性质和正方形的性质是解决问题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
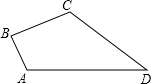如图，在四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，则△ACD是直角三角形．
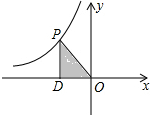如图，点P是反比例函数y=$\frac{k}{x}$（x＜0）图象上一点，过P向x轴作垂线，垂足为D，连接OP．若Rt△POD的面积为2，则k的值为（ ）
如图在平面直角坐标系中，△OAB的顶点坐标分别是O（0，0），A（2，4），B（6，0）．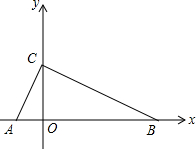
如图，已知Rt△ABC的斜边AB在x轴上，斜边上的高CO在y轴的正半轴上，且OA=1，OC=2，求经过A、B、C三点的二次函数解析式．
如图，直线y=$\frac{4}{3}$x与反比例函数的图象交于点A（3，a），第一象限内的点B在这个反比例函数图象上，OB与x轴正半轴的夹角为α，且tanα=$\frac{1}{3}$．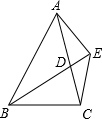
如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．则下列结论正确的是：①△ABD≌△EBC；②S△ABD=S△BDC；③∠BCE+∠BCD=180°；④AD=AE=EC；其中正确的是（ ）