题目内容
16. 如图,直线y=$\frac{4}{3}$x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$.
如图,直线y=$\frac{4}{3}$x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=$\frac{1}{3}$.(1)求点B的坐标;
(2)求△OAB的面积.
分析 (1)用直线求出点A坐标为(3,4),反比例函数解析式y=$\frac{12}{x}$,设点B坐标为(x,$\frac{12}{x}$),tanα=$\frac{1}{3}$,得出$\frac{12}{{x}^{2}}$=$\frac{1}{3}$,x=6,得出B点坐标(6,2);
(2)过A点做AC⊥x轴,交OB于点C,将三角形OAB分为两个三角形,分别求解即可.
解答 解:(1)∵直线y=$\frac{4}{3}$x与反比例函数的图象交于点A(3,a),
∴A(3,4),
反比例函数解析式y=$\frac{12}{x}$,
∵点B在这个反比例函数图象上,
设B(x,$\frac{12}{x}$),
∵tanα=$\frac{1}{3}$,
∴$\frac{\frac{12}{x}}{x}$=$\frac{1}{3}$,
解得:x=±6,
∵点B在第一象限,
∴x=6,
∴B(6,2).
答:点B坐标为(6,2).
(2)设直线OB为y=kx,(k≠0),
将点B(6,2)代入得:k=$\frac{1}{3}$,
∴OB直线解析式为:y=$\frac{1}{3}$x,
过A点做AC⊥x轴,交OB于点C,如下图: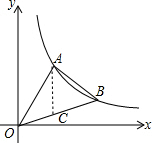
则点C坐标为:(3,1),
∴AC=3
S△OAB的面积
=S△OAC的面积+S△ACB的面积,
=$\frac{1}{2}$×|AC|×6
=9.
△OAB的面积为9.
点评 题目考查了一次函数与反比例函数的基本性质.求函数解析式及函数交点是函数常见问题.题目整体较为简单,学生在解决(2)中的面积问题可以利用多种方法求解.

练习册系列答案
相关题目
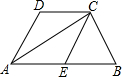 已知:如图所示,AB∥CD,AD∥CE,且∠ACB=90°,E为AB的中点.
已知:如图所示,AB∥CD,AD∥CE,且∠ACB=90°,E为AB的中点. 如图,BD与CE交于点A,AB=AC,AD=AE,△ABC的中线AN的反向延长线交DE于点M,求证:EM=DM.
如图,BD与CE交于点A,AB=AC,AD=AE,△ABC的中线AN的反向延长线交DE于点M,求证:EM=DM.