题目内容
7.解方程:(1)x2-4x-4=0;
(2)x(x-2)=15.
分析 (1)先计算判别式的值,然后利用求根公式解方程;
(2)先把方程化为一般式,然后利用因式分解法解方程.
解答 解:(1)△=b2-4ac=(-4)2-4×1×(-4)=32,
$x=\frac{{-(-4)±\sqrt{32}}}{2×1}$=$\frac{4±4\sqrt{2}}{2}$=2±$\sqrt{2}$,
所以x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$;
(2)原方程可变形为x2-2x-15=0,
(x-5)(x+3)=0,
x-5=0或x+3=0,
所以x1=5,x2=-3.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了公式法.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
15.2016年国家公务员考试报名人数约为1390000,将1390000用科学记数法表示,表示正确的为( )
| A. | 1.39×105 | B. | 1.39×106 | C. | 13.9×105 | D. | 13.9×106 |
19. 如图,把长方形ABCD沿EF对折后使两部分重合,若∠1=40°,则∠AEF=( )
如图,把长方形ABCD沿EF对折后使两部分重合,若∠1=40°,则∠AEF=( )
 如图,把长方形ABCD沿EF对折后使两部分重合,若∠1=40°,则∠AEF=( )
如图,把长方形ABCD沿EF对折后使两部分重合,若∠1=40°,则∠AEF=( )| A. | 100° | B. | 110° | C. | 115° | D. | 120° |
 如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=6,则正方形ADEF的边长为$\sqrt{13}$-1.
如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=6,则正方形ADEF的边长为$\sqrt{13}$-1.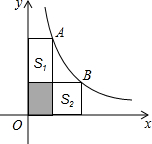 A、B两点在双曲线y=$\frac{5}{x}$上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=8.
A、B两点在双曲线y=$\frac{5}{x}$上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=8.