Question

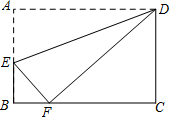如图，长方形ABCD中，点E在边AB上，将一边AD折叠，使点A恰好落在边BC的点F处，折痕为DE．若AB=4，BF=2，则AE的长是

 

．

Answer 1

考点：翻折变换（折叠问题）

专题：

分析：设AE=x，表示出BE，根据翻折变换的性质可得EF=AE，然后利用勾股定理列出方程求解即可．

解答：解：设AE=x，则BE=AB-AE=4-x，
∵折叠后点A恰好落在边BC的点F处，
∴EF=AE=x，
在Rt△BEF中，由勾股定理得，BE²+BF²=EF²，
即（4-x）²+2²=x²，
解得x=

5

2

，
即AE的长为

5

2

．
故答案为：

5

2

．

点评：本题考查了翻折变换的性质，勾股定理，此类题目熟记性质并利用勾股定理列出方程是解题的关键．