题目内容
 如图,直线yy1=x-1与直线y2=-
如图,直线yy1=x-1与直线y2=-| 1 |
| 2 |
(1)求点B的坐标及两直线与坐标轴围成的四边形ABCO的面积;
(2)连接AC,P(-1,a)为坐标系中的一个动点,是否存在点P,使得△PAC和△OAC的面积相等?若存在求出a的值,若不存在说明理由.
考点:一次函数综合题
专题:综合题
分析:(1)联立
,解该方程组就可得到点B的坐标;过点B作BE⊥y轴于点E,点B作BF⊥x轴于点F,连接OB,如图1,易得BE、BF、OA、OC的长,然后用割补法就可解决问题;
(2)由△PAC和△OAC的面积相等可证到OP∥AC,然后用待定系数法求出AC的解析式,从而得到OP的解析式,就可求出a的值.
|
(2)由△PAC和△OAC的面积相等可证到OP∥AC,然后用待定系数法求出AC的解析式,从而得到OP的解析式,就可求出a的值.
解答:解:(1)联立
,
解得:
,
∴点B的坐标为(2,1).
过点B作BE⊥y轴于点E,点B作BF⊥x轴于点F,连接OB,如图1,
则有BE=2,BF=1.
∵直线y1=x-1与x轴的交点是A,直线y2=-
x+2与y轴的交点是C,
∴点A的坐标为(1,0),点C的坐标为(0,2),
∴OA=1,OC=2,
∴S四边形OABC=S△OAB+S△OCB
=
OA•BF+
OC•BE
=
×1×1+
×2×2
=
.
(2)∵点P的坐标为(-1,a),
∴点P在直线x=-1上,如图2.
设直线AC的解析式为y=kx+b,
∵点A的坐标为(1,0),点C的坐标为(0,2),
∴
,
解得:
,
∴直线AC的解析式为y=-2x+2.
∵S△PAC=S△OAC,
∴点P、点O到AC的距离相等,
∴OP∥AC,
∴直线OP的解析式为y=-2x,
∴a=-2×(-1)=2,
∴a的值是2.
|
解得:
|
∴点B的坐标为(2,1).
过点B作BE⊥y轴于点E,点B作BF⊥x轴于点F,连接OB,如图1,

则有BE=2,BF=1.
∵直线y1=x-1与x轴的交点是A,直线y2=-
| 1 |
| 2 |
∴点A的坐标为(1,0),点C的坐标为(0,2),
∴OA=1,OC=2,
∴S四边形OABC=S△OAB+S△OCB
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 5 |
| 2 |
(2)∵点P的坐标为(-1,a),
∴点P在直线x=-1上,如图2.

设直线AC的解析式为y=kx+b,
∵点A的坐标为(1,0),点C的坐标为(0,2),
∴
|
解得:
|
∴直线AC的解析式为y=-2x+2.
∵S△PAC=S△OAC,
∴点P、点O到AC的距离相等,
∴OP∥AC,
∴直线OP的解析式为y=-2x,
∴a=-2×(-1)=2,
∴a的值是2.
点评:本题主要考查了用待定系数法求直线的解析式、等积变换、解方程组等知识,运用割补法是解决第(1)小题的关键,运用等积变换是解决第(2)小题的关键.

练习册系列答案
相关题目
在-2,+3.5,0,-
,-0.7,11中,负分数有( )
| 2 |
| 3 |
| A、l个 | B、2个 | C、3个 | D、4个 |
把ad=bc写成比例式,写错的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列运用等式的性质,变形不正确的是( )
| A、若x=y,则x+5=y+5 | ||||
| B、若a=b,则ac=bc | ||||
C、若
| ||||
D、若x=y,则
|
 根据二次函数y=x2+3x-4的图象回答:
根据二次函数y=x2+3x-4的图象回答: 如图,在四边形ACDE中,AE⊥AC于A,BF⊥AC于B,CD⊥AC于C,若AE=1.5m,BF=3.2m,AB=3m,BC=9m.求CD的长.
如图,在四边形ACDE中,AE⊥AC于A,BF⊥AC于B,CD⊥AC于C,若AE=1.5m,BF=3.2m,AB=3m,BC=9m.求CD的长.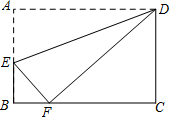 如图,长方形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE.若AB=4,BF=2,则AE的长是
如图,长方形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE.若AB=4,BF=2,则AE的长是