题目内容
已知点A在数轴上对应的数为a,点B对应的数为b,且|a+4|+(b-1)2=0,A,B之间的距离记作|AB|.
(1)设点P在数轴上对应的数为x,当|PA|-|PB|=2时,求x的值;
(2)若点P在A的左侧,M,N分别是PA,PB的中点,当点P在A的左侧移动时,式子|PN|-|PM|的值是否发生改变?若不变,请求其值;若发生变化,请说明理由.
(1)设点P在数轴上对应的数为x,当|PA|-|PB|=2时,求x的值;
(2)若点P在A的左侧,M,N分别是PA,PB的中点,当点P在A的左侧移动时,式子|PN|-|PM|的值是否发生改变?若不变,请求其值;若发生变化,请说明理由.
考点:数轴
专题:
分析:(1))由|a+4|+(b-1)2=0,得出a+4=0,b-1=0求出a,b的值,应考虑到A、B、P三点之间的位置关系的多种可能解题;
(2)当P在A的左侧移动时,设点P对应的数为x,列式求出|PN|-|PM|的值即可.
(2)当P在A的左侧移动时,设点P对应的数为x,列式求出|PN|-|PM|的值即可.
解答:解:(1)当P在点A左侧时,
|PA|-|PB|=-(|PB|-|PA|)=-|AB|=-5≠2.
当P在点B右侧时,
|PA|-|PB|=|AB|=5≠2.
∴上述两种情况的点P不存在.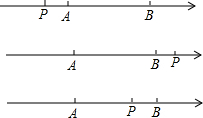
当P在A、B之间时,|PA|=|x-(-4)|=x+4,|PB|=|x-1|=1-x,
∵|PA|-|PB|=2,∴x+4-(1-x)=2.
∴x=-
,即x的值为-
;
(2)|PN|-|PM|的值不变,值为
.
∵|PN|-|PM|=
|PB|-
|PA|=
(|PB|-|PA|)=
|AB|=
,
∴|PN|-|PM|=
.
|PA|-|PB|=-(|PB|-|PA|)=-|AB|=-5≠2.
当P在点B右侧时,
|PA|-|PB|=|AB|=5≠2.
∴上述两种情况的点P不存在.
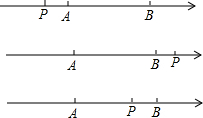
当P在A、B之间时,|PA|=|x-(-4)|=x+4,|PB|=|x-1|=1-x,
∵|PA|-|PB|=2,∴x+4-(1-x)=2.
∴x=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)|PN|-|PM|的值不变,值为
| 5 |
| 2 |
∵|PN|-|PM|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴|PN|-|PM|=
| 5 |
| 2 |
点评:本题考查了数轴的性质,由于引进了数轴,我们把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
把ad=bc写成比例式,写错的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若函数y=(m+3)x|m|-1+3x-4是二次函数,则m的值为( )
| A、3 | B、3或-3 |
| C、-3 | D、2或-2 |
绝对值比2大的数是( )
| A、-3 | B、0 | C、1 | D、2 |
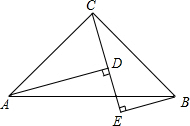 如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2cm,则BE的长为
如图,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于D,AD=5cm,DE=2cm,则BE的长为 根据二次函数y=x2+3x-4的图象回答:
根据二次函数y=x2+3x-4的图象回答: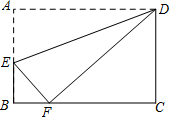 如图,长方形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE.若AB=4,BF=2,则AE的长是
如图,长方形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE.若AB=4,BF=2,则AE的长是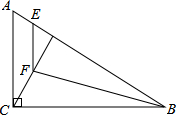 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.