题目内容
2.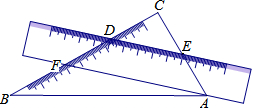 一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )| A. | 40° | B. | 45° | C. | 50° | D. | 10° |
分析 先根据∠CDE=40°,得出∠CED=50°,再根据DE∥AF,即可得到∠CAF=50°,最后根据∠BAC=60°,即可得出∠BAF的大小.
解答 解:由图可得,∠CDE=40°,∠C=90°,
∴∠CED=50°,
又∵DE∥AF,
∴∠CAF=50°,
∵∠BAC=60°,
∴∠BAF=60°-50°=10°,
故选:D.
点评 本题主要考查了平行线的性质以及三角形内角和定理的运用,解题时注意:两直线平行,同位角相等.

练习册系列答案
相关题目
10.某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0,每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12),符合关系式x=2n2-2kn+9(k+3)(k为常数),且得到了表中的数据.
(1)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.
| 月份n(月) | 1 | 2 |
| 成本y(万元/件) | 11 | 12 |
| 需求量x(件/月) | 120 | 100 |
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.
7.关于$\sqrt{8}$的叙述不正确的是( )
| A. | $\sqrt{8}$=2$\sqrt{2}$ | B. | 面积是8的正方形的边长是$\sqrt{8}$ | ||
| C. | $\sqrt{8}$是有理数 | D. | 在数轴上可以找到表示$\sqrt{8}$的点 |
14.下列运算正确的是( )
| A. | 3a2+a=3a3 | B. | 2a3•(-a2)=2a5 | C. | 4a6+2a2=2a3 | D. | (-3a)2-a2=8a2 |
 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹. 如图,四边形ABCD是正方形,△EBC是等边三角形.
如图,四边形ABCD是正方形,△EBC是等边三角形. 已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.