题目内容
12.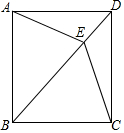 已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.
分析 (1)首先证得△ADE≌△CDE,由全等三角形的性质可得∠ADE=∠CDE,由AD∥BC可得∠ADE=∠CBD,易得∠CDB=∠CBD,可得BC=CD,易得AD=BC,利用平行线的判定定理可得四边形ABCD为平行四边形,由AD=CD可得四边形ABCD是菱形;
(2)由BE=BC可得△BEC为等腰三角形,可得∠BCE=∠BEC,利用三角形的内角和定理可得∠CBE=180×$\frac{1}{4}$=45°,易得∠ABE=45°,可得∠ABC=90°,由正方形的判定定理可得四边形ABCD是正方形.
解答 证明:(1)在△ADE与△CDE中,
$\left\{\begin{array}{l}{AD=CD}\\{DE=DE}\\{EA=EC}\end{array}\right.$,
∴△ADE≌△CDE,
∴∠ADE=∠CDE,
∵AD∥BC,
∴∠ADE=∠CBD,
∴∠CDE=∠CBD,
∴BC=CD,
∵AD=CD,
∴BC=AD,
∴四边形ABCD为平行四边形,
∵AD=CD,
∴四边形ABCD是菱形;
(2)∵BE=BC
∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,
∴∠CBE=180×$\frac{2}{2+3+3}$=45°,
∵四边形ABCD是菱形,
∴∠ABE=45°,
∴∠ABC=90°,
∴四边形ABCD是正方形.
点评 本题主要考查了正方形与菱形的判定及性质定理,熟练掌握定理是解答此题的关键.

练习册系列答案
相关题目
2.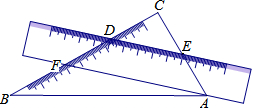 一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
 一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )| A. | 40° | B. | 45° | C. | 50° | D. | 10° |
20.数据2、5、6、0、6、1、8的中位数和众数分别是( )
| A. | 0和6 | B. | 0和8 | C. | 5和6 | D. | 5和8 |
17.八年级某同学6次数学小测验的成绩分别为:80分,85分,95分,95分,95分,100分,则该同学这6次成绩的众数和中位数分别是( )
| A. | 95分,95分 | B. | 95分,90分 | C. | 90分,95分 | D. | 95分,85分 |
1.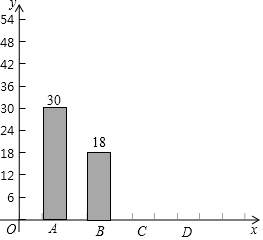 深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
(1)学生共120人,x=0.25,y=0.2;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有500人.
 深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.| 类型 | 频数 | 频率 |
| A | 30 | x |
| B | 18 | 0.15 |
| C | m | 0.40 |
| D | n | y |
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有500人.




 某企业今年第一季度各月份产值占这个季度总产值的百分比如图所示,又知二月份产值是72万元,那么该企业第一季度月产值的平均数是80万元.
某企业今年第一季度各月份产值占这个季度总产值的百分比如图所示,又知二月份产值是72万元,那么该企业第一季度月产值的平均数是80万元.