题目内容
11. 如图,四边形ABCD是正方形,△EBC是等边三角形.
如图,四边形ABCD是正方形,△EBC是等边三角形.(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.
分析 (1)根据正方形、等边三角形的性质,可以得到AB=BE=CE=CD,∠ABE=∠DCE=30°,由此即可证明;
(2)只要证明∠EAD=∠ADE=15°,即可解决问题;
解答  (1)证明:∵四边形ABCD是正方形,△ABC是等边三角形,
(1)证明:∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
$\left\{\begin{array}{l}{AB=DC}\\{∠ABE=∠DCE}\\{BE=CE}\end{array}\right.$,
∴△ABE≌△DCE(SAS).
(2)∵BA=BE,∠ABE=30°,
∴∠BAE=$\frac{1}{2}$(180°-30°)=75°,
∵∠BAD=90°,
∴∠EAD=90°-75°=15°,同理可得∠ADE=15°,
∴∠AED=180°-15°-15°=150°.
点评 本题考查正方形的性质、全等三角形 的判定和性质、等边三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.属于中考常考题型.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
2.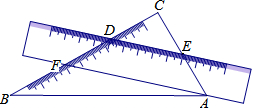 一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
 一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )| A. | 40° | B. | 45° | C. | 50° | D. | 10° |
6. 如图,直线a∥b,∠1=50°,则∠2的度数是( )
如图,直线a∥b,∠1=50°,则∠2的度数是( )
 如图,直线a∥b,∠1=50°,则∠2的度数是( )
如图,直线a∥b,∠1=50°,则∠2的度数是( )| A. | 130° | B. | 50° | C. | 40° | D. | 150° |
20.数据2、5、6、0、6、1、8的中位数和众数分别是( )
| A. | 0和6 | B. | 0和8 | C. | 5和6 | D. | 5和8 |
1.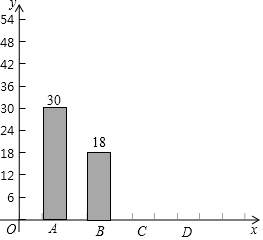 深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
(1)学生共120人,x=0.25,y=0.2;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有500人.
 深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.| 类型 | 频数 | 频率 |
| A | 30 | x |
| B | 18 | 0.15 |
| C | m | 0.40 |
| D | n | y |
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有500人.
 宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=$\left\{\begin{array}{l}7.5x({0≤x≤4})\\ 5x+10({4<x≤14})\end{array}$.
宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=$\left\{\begin{array}{l}7.5x({0≤x≤4})\\ 5x+10({4<x≤14})\end{array}$.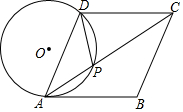 如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.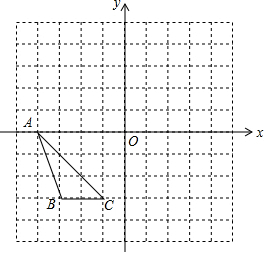 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.


