题目内容
17.某公司适应市场需要,准备开发1200件新产品投放市场,现由甲、乙两个工厂来加工生产,已知甲工厂每天的加工生产能力是乙工厂每天加工生产能力的1.5倍,并且加工生产480件该产品甲工厂比乙工厂少用8天.(1)求甲、乙两个工厂每天分别可加工生产多少件新产品?
(2)若甲工厂每天的加工生产成本为3万元,乙工厂每天的加工生产成本为1.8万元,且乙工厂最多可生产33天,要使加工生产这批新产品的总成本不高于114万元,你有哪几种安排生产的方案?(为不浪费工期,每个工厂生产的天数必须短)
分析 (1)先设乙工厂每天可加工生产x件新产品,则甲工厂每天可加工生产1.5x件新产品,根据加工生产480件新产品甲工厂比乙工厂少用8天,列出方程,求出x的值,再进行检验即可求出答案;
(2)设甲工厂加工生产y天,根据加工生产这批新产品的总成本不高于114万元,列出不等式,求出不等式的解集即可.
解答 解:(1)设乙工厂每天可加工生产x件新产品,则甲工厂每天可加工生产1.5x件新产品,根据题意可得:
$\frac{480}{x}$=$\frac{480}{1.5x}$+8,
解得:x=20,
经检验,x=20是原方程的根,也符合题意,
则1.5x=30,
答:甲工厂每天可加工生产30件新产品,乙工厂每天可加工生产20件新产品;
(2)设甲工厂加工生产y天,根据题意得:
$\left\{\begin{array}{l}{3y+1.8×\frac{1200-30y}{20}≤114}\\{\frac{1200-30y}{20}≤33}\end{array}\right.$,
解得:18≤y≤20,
安排生产的方案:①甲工厂加工生产18天,乙工厂加工生产33天;②甲工厂加工生产19天,乙工厂加工生产32天;③甲工厂加工生产20天,乙工厂加工生产30天.
点评 此题考查了分式方程的应用和一元一次不等式的应用,读懂题意,找出题目中的数量关系,列出方程和不等式,注意分式方程要检验.

练习册系列答案
相关题目
5.端午节前夕,在东昌湖举行的第七届全民健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所划行的路程y(m)与时间x(min)之间的函数关系如图所示,下列说法错误的是( )
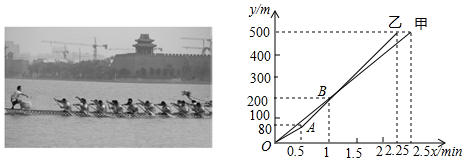

| A. | 乙队比甲队提前0.25min到达终点 | |
| B. | 当乙队划行110m时,此时落后甲队15m | |
| C. | 0.5min后,乙队比甲队每分钟快40m | |
| D. | 自1.5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min |
2.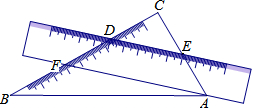 一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
 一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )
一把直尺和一块三角板ABC(含30°、60°角)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CDE=40°,那么∠BAF的大小为( )| A. | 40° | B. | 45° | C. | 50° | D. | 10° |
6. 如图,直线a∥b,∠1=50°,则∠2的度数是( )
如图,直线a∥b,∠1=50°,则∠2的度数是( )
 如图,直线a∥b,∠1=50°,则∠2的度数是( )
如图,直线a∥b,∠1=50°,则∠2的度数是( )| A. | 130° | B. | 50° | C. | 40° | D. | 150° |
 “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题:
“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题: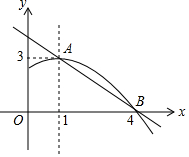 如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: 某企业今年第一季度各月份产值占这个季度总产值的百分比如图所示,又知二月份产值是72万元,那么该企业第一季度月产值的平均数是80万元.
某企业今年第一季度各月份产值占这个季度总产值的百分比如图所示,又知二月份产值是72万元,那么该企业第一季度月产值的平均数是80万元.