题目内容
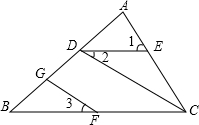 已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°.
已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°.请把下面证明过程及括号中的依据补充完整.
证明:∵∠1=∠ACB(已知)
∴
∴∠2=
∵∠2=∠3(已知)
∴∠3=
∴
∴∠BDC+∠DGF=180°(
考点:平行线的判定与性质
专题:推理填空题
分析:根据平行线的判定推出DE∥BC,根据平行线的性质推出∠2=∠BCD,求出∠3=∠BCD,根据平行线的判定得出DC∥FG,根据平行线的性质得出即可.
解答:证明:∵∠1=∠ACB,
∴DE∥BC(同位角相等,两条直线平行),
∴∠2=∠BCD(两直线平行,内错角相等),
∵∠2=∠3,
∴∠3=∠BCD(等量代换),
∴DC∥FG(同位角相等,两条直线平行),
∴∠BDC+∠DGF=180°(两直线平行,同旁内角互补),
故答案为:DE∥BC,同位角相等,两条直线平行,∠BCD,两直线平行,内错角相等,∠BCD,DC∥FG,同位角相等,两条直线平行,两直线平行,同旁内角互补.
∴DE∥BC(同位角相等,两条直线平行),
∴∠2=∠BCD(两直线平行,内错角相等),
∵∠2=∠3,
∴∠3=∠BCD(等量代换),
∴DC∥FG(同位角相等,两条直线平行),
∴∠BDC+∠DGF=180°(两直线平行,同旁内角互补),
故答案为:DE∥BC,同位角相等,两条直线平行,∠BCD,两直线平行,内错角相等,∠BCD,DC∥FG,同位角相等,两条直线平行,两直线平行,同旁内角互补.
点评:本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知两圆的半径为方程2x2-5x+2=0的两根,圆心距为
,则这两个圆的公切线有( )
| 3 |
| A、1条 | B、2条 | C、3条 | D、4条 |
抛物线y=x2+2x+c的顶点在第二象限,则c的取值范围是( )
| A、c<1 | B、c≤1 |
| C、c>1 | D、c≥1 |
下列各式中当x为0时,分式的值为0的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?
有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?