题目内容
先化简,再求值.
(-3x2-4xy)-2(-2x2-5xy+y)+(x2-5y),其中x,y满足(x+2)2+|y-1|=0.
(-3x2-4xy)-2(-2x2-5xy+y)+(x2-5y),其中x,y满足(x+2)2+|y-1|=0.
考点:整式的加减—化简求值,非负数的性质:绝对值,非负数的性质:偶次方
专题:计算题
分析:原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入原式计算即可得到结果.
解答:解:原式=-3x2-4xy+4x2+10xy-2y+x2-5y=2x2+6xy-7y,
∵(x+2)2+|y-1|=0,
∴x=-2,y=1,
则原式=8-12-7=-11.
∵(x+2)2+|y-1|=0,
∴x=-2,y=1,
则原式=8-12-7=-11.
点评:此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )| A、a>0 |
| B、当x≥1时,y随x的增大而增大 |
| C、c<0 |
| D、当-1<x<3时,y>0 |
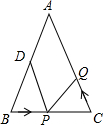 如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.
如图,在△ABC中,AB=AC=10,BC=8,点D为AB的中点,如果点P在线段BC上以每秒3个单位长度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动.在某一时刻,△BPD与△CQP全等,此时点Q的运动速度为每秒( )个单位长度.| A、3 | ||
B、
| ||
| C、3或3.75 | ||
| D、2或3 |
 如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )
如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,不正确的是( )| A、a>0 |
| B、b>0 |
| C、c<0 |
| D、b2-4ac>0 |
抛物线y=-
(x+1)2的对称轴是( )
| 1 |
| 2 |
A、直线x=
| ||
| B、直线x=1 | ||
| C、直线x=-1 | ||
| D、直线x=2 |
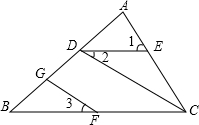 已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°.
已知:如图,∠1=∠ACB,∠2=∠3,求证:∠BOC+∠DGF=180°. 如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx<kx+b<mx+2的解集是
如图,直线y1=kx+b过点A(0,2),且与直线y2=mx交于点P(1,m),则不等式组mx<kx+b<mx+2的解集是